
【題目】某商場購進一批單價為16元的日用品.若按每件23元的價格銷售,每月能賣出270件;若按每件28元的價格銷售,每月能賣出120件;若規定售價不得低于23元,假定每月銷售件數y(件)與價格x(元/件)之間滿足一次函數.
(1)試求y與x之間的函數關系式.
(2)在商品不積壓且不考慮其他因素的條件下,銷售價格定為多少時,才能使每月的毛利潤w最大?每月的最大毛利潤為多少?
(3)若要使某月的毛利潤為1800元,售價應定為多少元?
【答案】(1)y=-30x+960;(2)24元,1920元;(3)26元
【解析】
試題(1)設y=kx+b,把(23,270)、(28,120)代入根據待定系數法即可求得結果;
(2)根據總利潤=單利潤×銷售量即可得到函數關系式,再根據二次函數的性質即可求得結果;
(3)根據毛利潤為1800元即可列方程求解,最后注意解的取舍.
(1)設y=kx+b,把(23,270)、(28,120)代入解得y=-30x+960;
(2)w="(x-16)(-30x+960)" =-30(x-24)2+1920,當x=24時,w有最大值1920
∴銷售價格定為24元時,才能使每月的毛利潤最大,最大毛利潤為1920元;
(3)當![]() 時,即
時,即![]()
解得![]() (舍去),
(舍去),![]()
∴某月的毛利潤為1800元,售價應定為26元.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】對于二次函數y=x2﹣3x+2和一次函數y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)稱為這兩個函數的“再生二次函數”,其中t是不為零的實數,其圖象記作拋物線L.現有點A(2,0)和拋物線L上的點B(﹣1,n),請完成下列任務:
(嘗試)
(1)當t=2時,拋物線y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)的頂點坐標為 ;
(2)判斷點A是否在拋物線L上;
(3)求n的值;
(發現)
通過(2)和(3)的演算可知,對于t取任何不為零的實數,拋物線L總過定點,坐標為 .
(應用)
二次函數y=﹣3x2+5x+2是二次函數y=x2﹣3x+2和一次函數y=﹣2x+4的一個“再生二次函數”嗎?如果是,求出t的值;如果不是,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
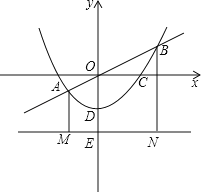
【題目】如圖,拋物線![]() (a≠0)經過A(-1,0),B(2,0)兩點,與y軸交于點C.
(a≠0)經過A(-1,0),B(2,0)兩點,與y軸交于點C.
(1)求拋物線的解析式及頂點D的坐標;
(2)點P在拋物線的對稱軸上,當△ACP的周長最小時,求出點P的坐標;
(3) 點N在拋物線上,點M在拋物線的對稱軸上,是否存在以點N為直角頂點的Rt△DNM與Rt△BOC相似,若存在,請求出所有符合條件的點N的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,四邊形ABCD中,AD∥BC,AD=CD,E是對角線BD上一點,且EA=EC.
(1)求證:四邊形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求證:四邊形ABCD是正方形.

查看答案和解析>>
科目:初中數學 來源: 題型:
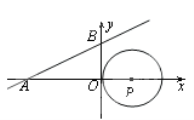
【題目】如圖,直線y=![]() x+
x+![]() 與x軸、y軸分別相交于A、B兩點,圓心P的坐標為(1,0),⊙P與y軸相切于點O.若將⊙P沿x軸向左移動,當⊙P與該直線相交時,滿足橫坐標為整數的點P的個數是( )
與x軸、y軸分別相交于A、B兩點,圓心P的坐標為(1,0),⊙P與y軸相切于點O.若將⊙P沿x軸向左移動,當⊙P與該直線相交時,滿足橫坐標為整數的點P的個數是( )
A.3B.4C.5D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠家一種摩托車如圖所示,它的大燈A射出的光線AB、AC與地面MN的夾角分別為8°和10°.
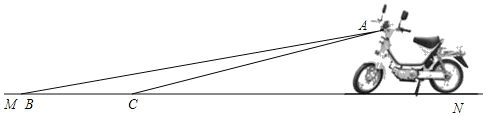
(1)該車大燈照亮地面的寬度BC是1.4m,求大燈A與地面距離約是多少?
(2)一般正常人從發現危險到做出剎車動作的反應時間是0.2s,從發現危險到摩托車完全停下所行駛的距離叫做最小安全距離,某人以60km/h的速度駕駛該車,突然遇到危險情況,立即剎車直到摩托車停止,在這個過程剎車距離是![]() m,請判斷(1)中的該車大燈A的地面高度是否能滿足最小安全距離的要去,若不能該如何調整A的高度?(參考數據:sin8°≈
m,請判斷(1)中的該車大燈A的地面高度是否能滿足最小安全距離的要去,若不能該如何調整A的高度?(參考數據:sin8°≈![]() ,tan8°≈
,tan8°≈![]() ,sin10°≈
,sin10°≈![]() ,tan10°≈
,tan10°≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】當x≤3時,函數y=x2﹣2x﹣3的圖象記為G,將圖象G在x軸上方的部分沿x軸翻折,圖象G的其余部分保持不變,得到一個新圖象M,若直線y=x+b與圖象M有且只有兩個公共點,則b的取值范圍是_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com