
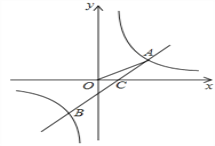
【題目】如圖,反比例函數y=![]() 與反比例函數y=k2
與反比例函數y=k2![]() +b的圖象的交點為A(m,1)、B(-2,n),OA與
+b的圖象的交點為A(m,1)、B(-2,n),OA與![]() 軸正方向的夾角為α,且tanα=
軸正方向的夾角為α,且tanα=![]() 。
。
(1)求反比例函數及一次函數的表達式;
(2)設直線AB與x軸交于點C,且AC與x軸正方向的夾角為β,求tanβ的值。
【答案】(1)直線AB的解析式為y=![]() x-1;(2)
x-1;(2)![]() .
.
【解析】試題分析:(1)用待定系數法求函數表達式,需要知道圖像上點的坐標,根據![]() ,構造直角三角形OAE,把三角函數值轉化為邊的比,可求出A點橫坐標,把A坐標代入
,構造直角三角形OAE,把三角函數值轉化為邊的比,可求出A點橫坐標,把A坐標代入![]() ,求得反比例函數解析式
,求得反比例函數解析式![]() ,把B坐標代入求出n=-2,把A、B坐標代入y=k2x+b即可求出一次函數解析式
,把B坐標代入求出n=-2,把A、B坐標代入y=k2x+b即可求出一次函數解析式![]() ;(2)易求C坐標(2,0),在Rt△ACE中,AE=1,CE=2,可求出tanβ的值.
;(2)易求C坐標(2,0),在Rt△ACE中,AE=1,CE=2,可求出tanβ的值.
試題解析:(1)過A作AE⊥x軸于E,∵tan∠AOE=tanα=![]() ,∴OE=4AE.又∵A(m,1),∴AE=1,AE=4,∴點A(4,1).∵A點在反比例函數
,∴OE=4AE.又∵A(m,1),∴AE=1,AE=4,∴點A(4,1).∵A點在反比例函數![]() 圖像上,∴k1=4,∴反比例函數為
圖像上,∴k1=4,∴反比例函數為![]() .∵B(-2,n)在反比例函數
.∵B(-2,n)在反比例函數![]() 圖像上,∴n="-2." ∴B的坐標是(-2,-2), 將A,B兩點的坐標代入直線y=k2x+b得:
圖像上,∴n="-2." ∴B的坐標是(-2,-2), 將A,B兩點的坐標代入直線y=k2x+b得: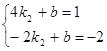 ,解得k2=
,解得k2=![]() ,b="-1," ∴直線AB的解析式為y=
,b="-1," ∴直線AB的解析式為y=![]() x-1;
x-1;
(2)∵直線AB的表達式為y=![]() x-1,令y=0,得x="2," ∴C(2,0), 又∵A(4,1),∴CE=2,AE=1.
x-1,令y=0,得x="2," ∴C(2,0), 又∵A(4,1),∴CE=2,AE=1.
∴tanβ=![]() =
=![]() .
.



 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】中國古代數學家們對于勾股定理的發現和證明,在世界數學史上具有獨特的貢獻和地位,體現了數學研究中的繼承和發展.現用4個全等的直角三角形拼成如圖所示“弦圖”.Rt△ABC中,∠ACB=90°,若![]() ,請你利用這個圖形解決下列問題:
,請你利用這個圖形解決下列問題:
(1)試說明![]() ;
;
(2)如果大正方形的面積是10,小正方形的面積是2,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校初二年級在元旦匯演中需要外出租用同一種服裝若干件,已知在沒有任何優惠的情況下,甲服裝店租用2件和在乙服裝店租用3件共需280元,在甲服裝店租用4件和在乙服裝店租用一件共需260元.
(1)求兩個服裝店提供的單價分別是多少?
(2)若該種服裝提前一周訂貨則甲乙兩個租售店都可以給予優惠,具體辦法如下:甲服裝店按原價的八折進行優惠;在乙服裝店如果租用5件以上,且超出5件的部分可按原價的六折進行優惠;設需要租用x件服裝,選擇甲店則需要y1元,選擇乙店則需要y2元,請分別求出y1,y2關于x的函數關系式;
(3)若租用的服裝在5件以上,請問租用多少件時甲乙兩店的租金相同?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】端午節期間,某食品店平均每天可賣出300只粽子,賣出1只粽子的利潤是1元.經調查發現,零售單價每降0.1元,每天可多賣出100只粽子.為了使每天獲取的利潤更多,該店決定把零售單價下降m(0<m<1)元.
(1)零售單價下降m元后,該店平均每天可賣出___只粽子,利潤為___元;
(2)在不考慮其他因素的條件下,當m定為多少時,才能使該店每天獲取的利潤是420元,并且賣出的粽子更多?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】通過學習同學們已經體會到靈活運用整式乘法公式給計算和化簡帶來的方便、快捷.相信通過下面材料的學習、探究,會使你大開眼界,并獲得成功的喜悅.
例:用簡便方法計算195×205.
解:195×205
=(200-5)(200+5) ①
=2002-52 ②
=39975.
(1)例題求解過程中,第②步變形是利用____________(填乘法公式的名稱);
(2)用簡便方法計算:
①9×11×101×10 001;
②(2+1)(22+1)(24+1)…(232+1)+1.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形網格中,每個小正方形的邊長均為1個單位長度,△ABC的三個頂點的位置如圖所示,現將△ABC平移,使點A變換為點A′,點B′、C′分別是B、C的對應點.

(1)請畫出平移后的△A′B′C′,并求△A′B′C′的面積;
(2)若連接AA′,CC′,則這兩條線段之間的關系是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩個同學分解因式x2+ax+b時,甲看錯了b,分解結果為(x+2)(x+4),乙看錯了a,分解結果為(x+1)(x+9),則2a+b=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A,B,C在同一直線上,在這條直線同側作等邊△ABD和等邊△BCE,連接AE和CD,交點為M,AE交BD于點P,CD交BE于點Q,連接PQ、BM, 有4個結論:①△ABE≌△DBC,②△DQB≌△ABP,③∠EAC=30°,④∠AMC=120°,請將所有正確結論的序號填在橫線上______.
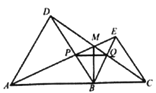
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com