
【題目】如圖,排球運動員站在點O處練習發球,將球從O點正上方2m的A處發出,把球看成點,其運行的高度y(m)與運行的水平距離x(m)滿足關系式y=a(x![]() k)2+h.已知球與O點的水平距離為6m時,達到最高2.6m,球網與O點的水平距離為9m.高度為2.43m,球場的邊界距O點的水平距離為18m,則下列判斷正確的是( )
k)2+h.已知球與O點的水平距離為6m時,達到最高2.6m,球網與O點的水平距離為9m.高度為2.43m,球場的邊界距O點的水平距離為18m,則下列判斷正確的是( )
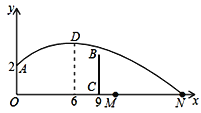
A. 球不會過網 B. 球會過球網但不會出界
C. 球會過球網并會出界 D. 無法確定
 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:初中數學 來源: 題型:
【題目】我們規定:形如![]() 為常數,
為常數,![]() 的函數叫做“奇特函數”.當
的函數叫做“奇特函數”.當![]() 時,“奇特函數”
時,“奇特函數”![]() 就是反比例函數
就是反比例函數![]() .
.
(1) 若矩形的兩邊長分別是2和3,當這兩邊長分別增加x和y后,得到的新矩形的面積為8 ,求y與x之間的函數關系式,并判斷這個函數是否為“奇特函數”;
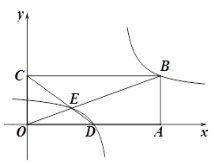
(2) 如圖,點O為坐標原點,矩形OABC的頂點A,C的坐標分別為(9,0)、(0,3).點D是OA的中點,連結OB,CD交于點E,“奇特函數”![]() 的圖象經過B,E兩點.
的圖象經過B,E兩點.
① 求這個“奇特函數”的解析式;
② 把反比例函數![]() 的圖象向右平移6個單位,再向上平移 個單位可得到①中所得“奇特函數”的圖象.過線段BE中點M的一條直線l與這個“奇特函數”的圖象交于P,Q兩點(P在Q的右側),若以B、E、P、Q為頂點組成的四邊形面積為16,請直接寫出點P的坐標.
的圖象向右平移6個單位,再向上平移 個單位可得到①中所得“奇特函數”的圖象.過線段BE中點M的一條直線l與這個“奇特函數”的圖象交于P,Q兩點(P在Q的右側),若以B、E、P、Q為頂點組成的四邊形面積為16,請直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】目前“微信”、“支付寶”、“共享單車”和“網購”給我們帶來了很多便利,初二數學小組在校內對“你最認可的四大新生事物”進行了調查,隨機調查了![]() 人(每名學生必選一種且只能從這四種中選擇一種)并將調查結果繪制成如下不完整的統計圖.
人(每名學生必選一種且只能從這四種中選擇一種)并將調查結果繪制成如下不完整的統計圖.

(1)根據圖中信息求出![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)請你幫助他們將這兩個統計圖補全;
(3)根據抽樣調查的結果,請估算全校2000名學生種,大約有多少人最認可“微信”這一新生事物?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一組數0,2,4,8,12,18,…中的奇數項和偶數項分別用代數式![]() ,
,![]() 表示,如第1個數為
表示,如第1個數為![]() ,第2個數為
,第2個數為![]() ,第3個數為
,第3個數為![]() ,…,則第8個數的值是_____,數軸上現有一點
,…,則第8個數的值是_____,數軸上現有一點![]() 從原點出發,依次以此組數中的數為距離向左右來回跳躍.第1秒時,點
從原點出發,依次以此組數中的數為距離向左右來回跳躍.第1秒時,點![]() 在原點,記為
在原點,記為![]() ;第2秒點
;第2秒點![]() 向左跳2個單位,記為
向左跳2個單位,記為![]() ,此時點
,此時點![]() 表示的數為-2;第3秒點
表示的數為-2;第3秒點![]() 向右跳4個單位,記為
向右跳4個單位,記為![]() ,點
,點![]() 表示的數為2;…按此規律跳躍,點
表示的數為2;…按此規律跳躍,點![]() 表示的數為_______.
表示的數為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以四邊形ABCD的邊AB、AD為底邊分別作等腰三角形ABE和等腰三角形ADF.
(1)當四邊形ABCD為正方形時(如圖①),以邊AB、AD為斜邊分別向外側作等腰直角△ABE和等腰直角△ADF,連接BF、ED,線段BF和ED的數量關系是_____________;
(2)當四邊形ABCD為矩形時(如圖②),以邊AB、AD為斜邊分別向矩形內側、外側作等腰直角△ABE和等腰直角△ADF,連接EF、BD,線段EF和BD具有怎樣的數量關系?請說明理由;
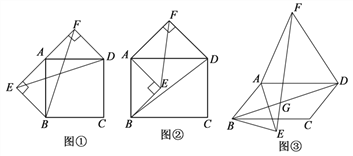
(3)當四邊形ABCD為平行四邊形時,以邊AB、AD為底邊分別向平行四邊形內側、外側作等腰△ABE和等腰△ADF,且△ABE和△ADF的頂角均為![]() ,連接EF、BD,交點為G.請用
,連接EF、BD,交點為G.請用![]() 表示出∠FGD,并說明理由.
表示出∠FGD,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 的頂點
的頂點![]() ,
,![]() ,點
,點![]() 在
在![]() 軸的正半軸上,按以下步驟作圖:①以點
軸的正半軸上,按以下步驟作圖:①以點![]() 為圓心、適當長度為半徑作弧,分別交
為圓心、適當長度為半徑作弧,分別交![]() 、
、![]() 于點
于點![]() ,
,![]() ;②分別以點
;②分別以點![]() ,
,![]() 為圓心、大于
為圓心、大于![]() 的長為半徑作弧,兩弧在
的長為半徑作弧,兩弧在![]() 內交于點
內交于點![]() ;③作射線
;③作射線![]() ,交邊
,交邊![]() 于點
于點![]() .則點
.則點![]() 的坐標為( )
的坐標為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(題文)停車難已成為合肥城市病之一,主要表現在居住停車位不足,停車資源結構性失衡,中心城區供需差距大等等.如圖是張老師的車與墻平行停放的平面示意圖,汽車靠墻一側OB與墻MN平行且距離為0.8米,已知小汽車車門寬AO為 1.2 米,當車門打開角度∠AOB為40°時,車門是否會碰到墻?請說明理由.(參考數據:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

查看答案和解析>>
科目:初中數學 來源: 題型:
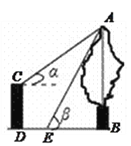
【題目】如圖,CD是一高為4米的平臺,AB是與CD底部相平的一棵樹,在平臺頂C點測得樹頂A點的仰角![]()
![]() ,從平臺底部向樹的方向水平前進3米到達點E,在點E處測得樹頂A點的仰角
,從平臺底部向樹的方向水平前進3米到達點E,在點E處測得樹頂A點的仰角![]() ,求樹高AB(結果保留根號).
,求樹高AB(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人玩“錘子、石頭、剪子、布”游戲,他們在不透明的袋子中放入形狀、大小均相同的15張卡片,其中寫有“錘子”、“石頭”、“剪子”、“布”的卡片張數分別為2,3,4,6.兩人各隨機摸出一張卡片(先摸者不放回)來比勝負,并約定:“錘子”勝“石頭”和“剪子”,“石頭”勝“剪子”,“剪子”勝“布”,“布”勝“錘子”和“石頭”,同種卡片不分勝負.
(1)若甲先摸,則他摸出“石頭”的概率是多少?
(2)若甲先摸出了“石頭”,則乙獲勝的概率是多少?
(3)若甲先摸,則他先摸出哪種卡片獲勝的可能性最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com