
如圖,在△ABC中,AB=BC,將△ABC繞點B順時針旋轉 度,得到△A1BC1,A1B交AC于點E,A1C1分別交AC、BC于點D、F,下列結論:①∠CDF=
度,得到△A1BC1,A1B交AC于點E,A1C1分別交AC、BC于點D、F,下列結論:①∠CDF= ,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE。其中正確的是________(寫出正確結論的序號)。
,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE。其中正確的是________(寫出正確結論的序號)。

①②⑤.
【解析】
試題分析:①兩個不同的三角形中有兩個角相等,那么第三個角也相等;
②根據ASA進而得出△A1BF≌△CBE,即可得出A1E=CF;
③∠CDF=α,而∠C與順時針旋轉的度數不一定相等,所以DF與FC不一定相等;
④AE不一定等于CD,則AD不一定等于CE,
⑤用角角邊證明△A1BF≌△CBE后可得A1F=CE.
試題解析:①∠C=∠C1(旋轉后所得三角形與原三角形完全相等)
又∵∠DFC=∠BFC1(對頂角相等)
∴∠CDF=∠C1BF=α,故結論①正確;
②∵AB=BC,
∴∠A=∠C,
∴∠A1=∠C,
在△A1BF和△CBE中

∴△A1BF≌△CBE(ASA),
∴BF=BE,
∴A1B-BE=BC-BF,
∴A1E=CF,故②正確;
③在三角形DFC中,∠C與∠CDF=α度不一定相等,所以DF與FC不一定相等,
故結論③不一定正確;
④∵AE不一定等于CD,
∴AD不一定等于CE,
故④錯誤.
⑤∠A1=∠C,BC=A1B,∠A1BF=∠CBE
∴△A1BF≌△CBE(ASA)
那么A1F=CE.
故結論⑤正確.
考點:1.旋轉的性質;2.全等三角形的判定與性質;3.等腰三角形的性質.


科目:初中數學 來源:2014-2015學年北京市七年級上學期期中檢測數學試卷(解析版) 題型:選擇題
過度包裝既浪費資源又污染環境.據測算,如果全國每年減少10%的過度包裝紙用量,那么可減排二氧化碳3120000噸.把數3120000用科學記數法表示為( ).
A.3.12×105 B.3.12×106 C.31.2×105 D.0.312×107
查看答案和解析>>
科目:初中數學 來源:2014-2015學年河北省廊坊市九年級上學期期中考試數學試卷(解析版) 題型:解答題
某校團委準備舉辦學生繪畫展覽,為美化畫面,在長為3 0cm、寬為20的矩形畫面四周鑲上寬度相等的彩紙,并使彩紙的面積恰好與原畫面面積相等(如圖),求彩紙的寬度.

查看答案和解析>>
科目:初中數學 來源:2014-2015學年河北省廊坊市九年級上學期期中考試數學試卷(解析版) 題型:選擇題
如圖,A、B、C是⊙O上的三點,已知∠O=60°,則∠C=( )
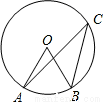
A、20° B、25° C、30° D、45°
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省九年級10月月考數學試卷(解析版) 題型:解答題
(本 題14分)已知矩形ABCD的頂點A與點O重合,AD、AB分別在x軸、y軸上,且AD=2,AB=3;拋物線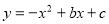 經過坐標原點O和x軸上另一點E(4,0)。
經過坐標原點O和x軸上另一點E(4,0)。
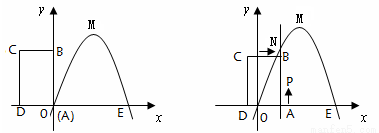
(1)當x取何值時,該拋物線的最大值是多少?
(2)將矩形ABCD以每秒1個單位長度的速度從圖1所示的位置沿x軸的正方向勻速平行移動,同時一動點P也以相同的速度從點A出發向B勻速移動.設它們運動的時間為t秒(0≤t≤3),直線AB與該拋物線的交點為N(如圖2所示)。
① 當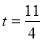 時,判斷點P是否在直線ME上,并說明理由;
時,判斷點P是否在直線ME上,并說明理由;
② 以P、N、C、D為頂點的多邊形面積是否可能為5,若有可能,求出此時N點的坐標;若無可能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com