
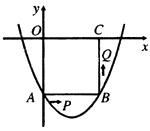
如圖在平面直角坐標系xoy中,正方形OABC的邊長為2厘米,點A、C分別在y軸的負半軸和x軸的正半軸上.拋物線y=ax2+bx+c經過點A ,B和點 D(4, 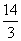 )
)
(1)求拋物線的解析式;
(2)如果點P由點A開始沿AB邊以2厘米/秒的速度向點B移動,同時點Q由B點開始沿BC邊以1厘米/秒的速度向點C移動.若P、Q中有一點到達終點,則另一點也停止運動,設P、Q兩點移動的時間為t秒,S=PQ2(厘米2)
寫出S與t之間的函數關系式,并寫出t的取值范圍,當t為何值時,S最小;
(3)當s取最小值時,在拋物線上是否存在點R,使得以P、B、Q、R為頂點的四邊形是平行四邊形?如果存在,求出點R的坐標;如果不存在,請說明理由.
(4)在拋物線的對稱軸上求出點M,使得M到D,A距離之差最大?寫出點M的坐標.
 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學課時作業系列答案
名牌中學課時作業系列答案科目:初中數學 來源: 題型:
【問題】如圖1、2是底面為1cm,母線長為2cm的圓柱體和圓錐體模型.現要用長為2πcm,寬為4cm的長方形彩紙(如圖3)裝飾圓柱、圓錐模型表面.已知一個圓柱和一個圓錐模型為一套,長方形彩紙共有122張,用這些紙最多能裝飾多少套模型呢?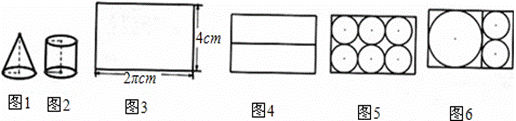
【對話】老師:“長方形紙可以怎么裁剪呢?”
學生甲:“可按圖4方式裁剪出2張長方形.”
學生乙:“可按圖5方式裁剪出6個小圓.”
學生丙:“可按圖6方式裁剪出1個大圓和2個小圓.”
老師:盡管還有其他裁剪方法,但為裁剪方便,我們就僅用這三位同學的裁剪方法!
【解決】(1)計算:圓柱的側面積是 4πcm2,圓錐的側面積是 2cm2.
(2)1張長方形彩紙剪拼后最多能裝飾 2個圓錐模型;5張長方形彩紙剪拼后最多能裝飾 6個圓柱體模型.
(3)求用122張彩紙對多能裝飾的圓錐、圓柱模型套數.
查看答案和解析>>
科目:初中數學 來源: 題型:
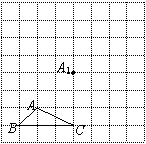
如圖所示,正方形網格中, 為格點三角形(即三角形的頂點都在格點上).
為格點三角形(即三角形的頂點都在格點上).
(1)把 沿
沿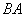 方向平移后,點
方向平移后,點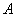 移到點
移到點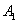 ,在網格中畫出平移后得到的
,在網格中畫出平移后得到的 ;
;
(2)把 繞點
繞點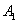 按逆時針方向旋轉
按逆時針方向旋轉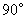 ,在網格中畫出旋轉后的
,在網格中畫出旋轉后的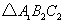 ;
;
(3)如果網格中小正方形的邊長為1,求點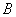 經過(1)、(2)變換的路徑總長.
經過(1)、(2)變換的路徑總長.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
已知點(x0,y0)是二次函數y=ax2+bx+c(a>0)的一個點,且x0滿足關于x的方程2ax+b=0,則下列選項正確的是( )
A、對于任意實數x都有y≥ y0 B、對于任意實數x都有y≤y0
C、對于任意實數x都有y>y0 D、對于任意實數x都有y<y0
查看答案和解析>>
科目:初中數學 來源: 題型:
2014年3月5日,第十二屆全國人民代表大會第二次會議在人民大會堂開幕,國務院總理李克強作《政府工作報告》。報告指出我國2013年國內生產總值達到569000億元。“569000”這個數據用科學記數法(保留兩個有效數字)表示正確的是:……………………( )
A.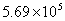 B.
B.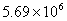 C.
C. D.
D.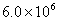
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com