【題目】如圖是二次函數y=ax2+bx+c的圖象的一部分，對稱軸是直線x=1． ①b2＞4ac；②b＜0；③y隨x的增大而減小；④若（﹣2，y1），（5，y2）是拋物線上的兩點，則y1＜y2 ， 上述4個判斷中，正確的是（ ）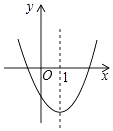
A.①②④
B.①④
C.①③④
D.②③④
【答案】A
【解析】解：∵圖象與x軸有2個交點， ∴b2﹣4ac＞0，b2＞4ac，故①正確；
∵﹣ 
=1，又a＞0，∴b＜0，故②正確；
當x＞1時，y隨x的增大而增大，故③錯誤；
由對稱軸為x=1，當x=﹣2時和x=4時，函數值相等，根據函數性質，x=5的函數值大于x=4的函數值，
∴y1＜y2 ， 故④正確．
所以正確的是①②④，
故選A．
【考點精析】利用二次函數圖象以及系數a、b、c的關系對題目進行判斷即可得到答案，需要熟知二次函數y=ax2+bx+c中，a、b、c的含義：a表示開口方向：a>0時，拋物線開口向上; a<0時，拋物線開口向下b與對稱軸有關：對稱軸為x=-b/2a;c表示拋物線與y軸的交點坐標：（0，c）．
同步輕松練習系列答案
課課通課程標準思維方法與能力訓練系列答案科目：初中數學 來源： 題型：
【題目】如圖，將矩形紙片ABCD沿對角線BD折疊，使點A落在平面上的F點處，DF交BC于點E．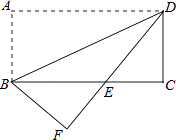 
（1）求證：△DCE≌△BFE；
（2）若CD=2，∠ADB=30°，求BE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AD⊥BC于D，BD=AD，DG=DC，E，F分別是BG，AC的中點．
（1）求證：DE=DF，DE⊥DF；
（2）連接EF，若AC=10，求EF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】函數 
的圖象如圖所示，則結論： ①兩函數圖象的交點A的坐標為（2，2）；
②當x＞2時，y2＞y1；
③當x=1時，BC=3；
④當x逐漸增大時，y1隨著x的增大而增大，y2隨著x的增大而減小．
其中正確結論的序號是 ．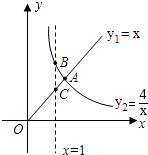 
查看答案和解析>>
科目：初中數學 來源： 題型：
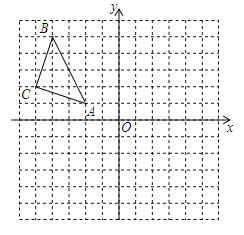
【題目】如圖，△ABC在平面直角坐標系中，點A、B、C的坐標分別為A（﹣2，1），B（﹣4，5），C（﹣5，2）．
（1）作△ABC關于y對稱的△A1B1C1，其中，點A、B、C的對應點分別為A1、B1、C1（不要求寫作法）；
（2）寫出點A1、B1、C1的坐標；
（3）計算△A1B1C1的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某地為提倡節約用水，準備實行自來水“階梯計費”方式，用戶用水不超出基本用水量的部分享受基本價格，超出基本用水量的部分實行加價收費，為更好地決策，自來水公司隨機抽取部分用戶的用適量數據，并繪制了如下不完整統計圖（每組數據包括右端點但不包括左端點），請你根據統計圖解決下列問題：
（1）此次調查抽取了多少用戶的用水量數據？
（2）補全頻數分布直方圖，求扇形統計圖中“25噸～30噸”部分的圓心角度數；
（3）如果自來水公司將基本用水量定為每戶25噸，那么該地20萬用戶中約有多少用戶的用水全部享受基本價格？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB＞AC，AD平分∠BAC
（1）尺規作圖：在AD上標出一點P，使得點P到點B和點C的距離相等（不寫作法，但必須保留作圖痕跡）；
（2）過點P作PE⊥AB于點E，PF⊥AC于點F，求證：BE=CF；
（3）若AB=a，AC=b，則BE= ，AE= ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
