
(本題滿分12分)△ABC是邊長為4個單位長度的等邊三角形,點F是邊BC上的點,FD⊥AB,FE⊥AC,

(1)求證:△BDF∽△CEF;
(2)已知A、D、F、E四點在同一個圓上,若tan∠EDF= ,求此圓的半徑.
,求此圓的半徑.
(3)設BF=m,四邊形ADFE面積為S,求出S與m之間的函數關系,并探究當m為何值時S取最大值;
(1)見解析;
(2)此圓半徑長為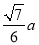 .
.
(3)S═﹣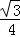 (m﹣2)2+3
(m﹣2)2+3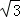 (其中0<m<4).當m=2時,S取到最大值,最大值為3
(其中0<m<4).當m=2時,S取到最大值,最大值為3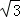 .
.
【解析】
試題分析:(1)只需找到兩組對應角相等即可.
(2)易知AF就是圓的直徑,利用圓周角定理將∠EDF轉化為∠EAF.在△AFC中,知道tan∠EAF、∠C、AC,通過解直角三角形就可求出AF長.
(3)四邊形ADFE面積S可以看成△ADF與△AEF的面積之和,借助三角函數用m表示出AD、DF、AE、EF的長,進而可以用含m的代數式表示S,然后通過配方,轉化為二次函數的最值問題,就可以解決問題.
試題解析:(1)∵DF⊥AB,EF⊥AC,
∴∠BDF=∠CEF=90°.
∵△ABC為等邊三角形,
∴∠B=∠C=60°.
∵∠BDF=∠CEF,∠B=∠C,
∴△BDF∽△CEF.
(2)如圖,
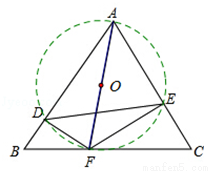
∵A、D、F、E四點共圓,
∴∠EDF=∠EAF.
∵∠ADF=∠AEF=90°,
∴AF是此圓的直徑.
∵tan∠EDF=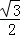 ,
,
∴tan∠EAF=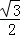 .
.
∴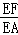 =
=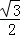 .
.
∵∠C=60°,
∴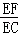 =tan60°=
=tan60°=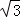 .
.
設EC=x,則EF=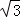 x,EA=2x.
x,EA=2x.
∵AC=a,
∴2x+x=a.
∴x=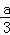 .
.
∴EF=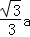 ,AE=
,AE=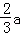 .
.
∵∠AEF=90°,
∴AF=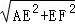 =
=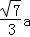 .
.
∴AO=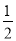 AF=
AF=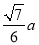
∴此圓半徑長為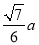 .
.
(3)∵∠BDF=90°,∠B=60°,
∴sin60°=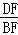 =
=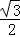 ,cos60°=
,cos60°=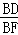 =
= .
.
∵BF=m,
∴DF=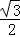 m,BD=
m,BD=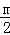 .
.
∵AB=4,
∴AD=4﹣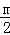 .
.
∴S△ADF= AD•DF
AD•DF
= ×(4﹣
×(4﹣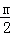 )×
)×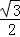 m
m
=﹣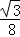 m2+
m2+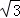 m.
m.
同理:S△AEF= AE•EF
AE•EF
= ×(4﹣
×(4﹣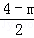 )×
)×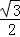 (4﹣m)
(4﹣m)
=﹣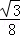 m2+2
m2+2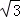 .
.
∴S=S△ADF+S△AEF
=﹣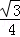 m2+
m2+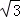 m+2
m+2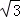
=﹣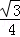 (m2﹣4m﹣8)
(m2﹣4m﹣8)
=﹣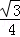 (m﹣2)2+3
(m﹣2)2+3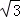 .其中0<m<4.
.其中0<m<4.
∵﹣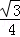 <0,0<2<4,
<0,0<2<4,
∴當m=2時,S取最大值,最大值為3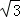 .
.
∴S與m之間的函數關系為:
S═﹣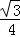 (m﹣2)2+3
(m﹣2)2+3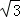 (其中0<m<4).
(其中0<m<4).
當m=2時,S取到最大值,最大值為3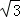 .
.
考點:相似形綜合題


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:初中數學 來源:2014-2015學年云南省景洪市九年級11月月考數學試卷(解析版) 題型:選擇題
如圖,在⊙O中,∠ABC=50°,則∠AOC等于( )

A.50° B.80° C.90° D.100°
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省等九年級上學期第三次月考數學試卷(解析版) 題型:填空題
如圖,□ABCD的面積為12,E為BC中點,DE、AC交于F點, 的面積為 .
的面積為 .

查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省等九年級上學期第三次月考數學試卷(解析版) 題型:選擇題
在 中,
中, ,如果把
,如果把 的各邊的長都縮小為原來的
的各邊的長都縮小為原來的 ,則
,則 的正切值( )
的正切值( )
A.縮小為原來的
B.擴大為原來的4倍
C.縮小為原來的
D.沒有變化
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省靖江市九年級1月獨立作業數學試卷(解析版) 題型:解答題
(本題滿分8分)已知:如圖,AB和DE是直立在地面上的兩根立柱,AB=5m,某一時刻,AB在陽光下的投影BC=4m.

(1)請你在圖中畫出此時DE在陽光下的投影;
(2)在測量AB的投影長時,同時測出DE在陽光下的投影長為6m,請你計算DE的長
查看答案和解析>>
科目:初中數學 來源:2014-2015學年天津市七年級上學期期末數學試卷(解析版) 題型:計算題
計算:(1)(+6.2)―(+4.6)―(―3.6)―(―2.8)
(2)1.6×(―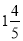 )×(―2.5)×(―
)×(―2.5)×(―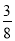 )
)
(3)(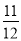 ―
―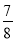 +
+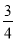 ―
―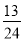 )×(―4.8)
)×(―4.8)
(4)(―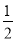 )2+(―1)101―0.25+(
)2+(―1)101―0.25+(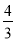 )2÷(―
)2÷(―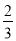 )3÷
)3÷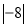
(5)(―2)3÷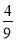 ×(―
×(―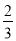 )2+
)2+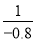 ―5×(―
―5×(―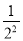 )
)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年天津市八年級上學期期末數學試卷(解析版) 題型:選擇題
如下圖,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正確的等式是( )
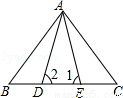
A.AB=AC B.∠BAE=∠CAD C.BE=DC D.AD=DE
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com