
【題目】某校要從新入學的兩名體育特長生李勇、張浩中挑選一人參加校際跳遠比賽,在跳遠專項測試以及以后的![]() 次跳遠選拔賽中,他們的成績(單位:
次跳遠選拔賽中,他們的成績(單位:![]() )如下表所示:
)如下表所示:
專項測試和 | 平均數 | 方差 | |||||||
李勇 |
|
|
|
|
|
|
|
| |
張浩 |
|
|
|
|
|
|
|
| |
![]() 求張浩同學
求張浩同學![]() 次測試成績的平均數,李勇同學
次測試成績的平均數,李勇同學![]() 次測試成績的方差;
次測試成績的方差;
![]() 請你分別從平均數和方差的角度分析兩人成績的特點;
請你分別從平均數和方差的角度分析兩人成績的特點;
![]() 經查閱歷屆比賽的資料,成績若達到
經查閱歷屆比賽的資料,成績若達到![]() ,就很可能得到冠軍,你認為應選誰去參賽奪冠軍比較有把握?說明理由;
,就很可能得到冠軍,你認為應選誰去參賽奪冠軍比較有把握?說明理由;
![]() 以往的該項最好成績的紀錄是
以往的該項最好成績的紀錄是![]() ,若要想打破紀錄,你認為應選誰去參賽?
,若要想打破紀錄,你認為應選誰去參賽?
【答案】(1)![]() ;(2)從成績的平均數來看,張浩成績的“平均水平”比李勇的高,從成績的方差來看,李勇的成績比張浩的穩定;(3)選李勇更有把握奪冠,理由見解析;(4)張浩,理由見解析
;(2)從成績的平均數來看,張浩成績的“平均水平”比李勇的高,從成績的方差來看,李勇的成績比張浩的穩定;(3)選李勇更有把握奪冠,理由見解析;(4)張浩,理由見解析
【解析】
(1)根據平均數、方差的概念計算即可;
(2)從平均數、方差的角度分析即可;
(3)根據方差,從成績的穩定性方面分析;
(4)從最高成績方面進行分析,超過6.15米的破紀錄的可能性大.
解:![]() 張浩成績的平均數為:
張浩成績的平均數為:![]() ,
,
李勇的方差為:![]() ;
;
專項測試和 | 中位數 | 平均數 | 方差 | |||||||
李勇 |
|
|
|
|
|
|
|
|
|
|
張浩 |
|
|
|
|
|
|
|
|
|
|
![]() 從成績的平均數來看,張浩成績的“平均水平”比李勇的高,從成績的方差來看,李勇的成績比張浩的穩定;
從成績的平均數來看,張浩成績的“平均水平”比李勇的高,從成績的方差來看,李勇的成績比張浩的穩定;
![]() 在跳遠專項測試以及之后的
在跳遠專項測試以及之后的![]() 次跳遠選拔賽中,李勇有
次跳遠選拔賽中,李勇有![]() 次成績超過
次成績超過![]() 米,而張浩只有兩次超過
米,而張浩只有兩次超過![]() 米,從成績的方差來看,李勇的成績比張浩的穩定,選李勇更有把握奪冠.
米,從成績的方差來看,李勇的成績比張浩的穩定,選李勇更有把握奪冠.
![]() 張浩有兩次成績為
張浩有兩次成績為![]() 米和
米和![]() 米,超過
米,超過![]() 米,而李勇沒有一次達到
米,而李勇沒有一次達到![]() 米,故選張浩.
米,故選張浩.


科目:初中數學 來源: 題型:
【題目】為慶祝中華人民共和國七十周年華誕,某校舉行書畫大賽,準備購買甲、乙兩種文具,獎勵在活動中表現優秀的師生.已知購買![]() 個甲種文具、
個甲種文具、![]() 個乙種文具共需花費
個乙種文具共需花費![]() 元;購買
元;購買![]() 個甲種文具、
個甲種文具、![]() 個乙種文具共需花費
個乙種文具共需花費![]() 元.
元.
(1)求購買一個甲種文具、一個乙種文具各需多少元?
(2)若學校計劃購買這兩種文具共![]() 個,投入資金不少于
個,投入資金不少于![]() 元又不多于
元又不多于![]() 元,設購買甲種文具
元,設購買甲種文具![]() 個,求有多少種購買方案?
個,求有多少種購買方案?
(3)設學校投入資金![]() 元,在(2)的條件下,哪種購買方案需要的資金最少?最少資金是多少元?
元,在(2)的條件下,哪種購買方案需要的資金最少?最少資金是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝店銷售一批襯衫,每件進價![]() 元,開始以每件
元,開始以每件![]() 元的價格銷售,每星期能賣出
元的價格銷售,每星期能賣出![]() 件,后來因庫存積壓,決定降價銷售,經兩次降價后的每件售價
件,后來因庫存積壓,決定降價銷售,經兩次降價后的每件售價![]() 元,每星期能賣出
元,每星期能賣出![]() 件.
件.
![]() 已知兩次降價百分率相同,求每次降價的百分率;
已知兩次降價百分率相同,求每次降價的百分率;
![]() 聰明的店主在降價過程中發現,適當的降價既可增加銷售又可增加收入,且每件襯衫售價每降低
聰明的店主在降價過程中發現,適當的降價既可增加銷售又可增加收入,且每件襯衫售價每降低![]() 元,銷售會增加
元,銷售會增加![]() 件,若店主想要每星期獲利
件,若店主想要每星期獲利![]() 元,應把售價定為多少元?
元,應把售價定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線C1:y1=mx2﹣4mx+2n﹣1與平行于x軸的直線交于A、B兩點,且A點坐標為(﹣1,2),請結合圖象分析以下結論:①對稱軸為直線x=2;②拋物線與y軸交點坐標為(0,﹣1);③m>![]() ;④若拋物線C2:y2=ax2(a≠0)與線段AB恰有一個公共點,則a的取值范圍是
;④若拋物線C2:y2=ax2(a≠0)與線段AB恰有一個公共點,則a的取值范圍是![]() ≤a<2;⑤不等式mx2﹣4mx+2n>0的解作為函數C1的自變量的取值時,對應的函數值均為正數,其中正確結論的個數有( )
≤a<2;⑤不等式mx2﹣4mx+2n>0的解作為函數C1的自變量的取值時,對應的函數值均為正數,其中正確結論的個數有( )
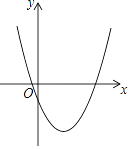
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應團中央“號召全國每位團員,少先隊員捐一瓶水”的倡議,我校師生積極開展了“情系西南災區”的捐款活動.某班![]() 名同學捐款的數額分別是(單位:元):
名同學捐款的數額分別是(單位:元):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .則這組數據的中位數和眾數分別是( )元.
.則這組數據的中位數和眾數分別是( )元.
A. 5,5 B. 10,5
C. 10,7.5 D. 7.5,5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數![]() 的圖象經過點
的圖象經過點![]() .
.
(1)若函數圖象經過原點,求k,b的值
(2)若點![]() 是該函數圖象上的點,當
是該函數圖象上的點,當![]() 時,總有
時,總有![]() ,且圖象不經過第三象限,求k的取值范圍.
,且圖象不經過第三象限,求k的取值范圍.
(3)點![]() 在函數圖象上,若
在函數圖象上,若![]() ,求n的取值范圍.
,求n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知等腰直角三角形ABC,點P是斜邊BC上一點(不與B,C重合),PE是△ABP的外接圓⊙O的直徑.
(1)求證:△APE是等腰直角三角形;
(2)若⊙O的直徑為2,求![]() 的值.
的值.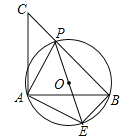
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 是
是![]() 的直徑,
的直徑,![]() ,
,![]() 、
、![]() 分別與圓相交于
分別與圓相交于![]() 、
、![]() ,那么下列等式中一定成立的是( )
,那么下列等式中一定成立的是( )
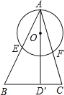
A. AEBF=AFCF B. AEAB=AOAD'
C. AEAB=AFAC D. AEAF=AOAD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,C是⊙O上一點,過點C的直線交AB的延長線于點D,AE⊥DC,垂足為E,F是AE與⊙O的交點,AC平分∠BAE.

(1)求證:DE是⊙O的切線;
(2)若AE=6,∠D=30°,求圖中陰影部分的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com