
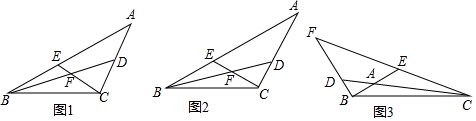
分析 (1)先判斷出∠BEC=∠CGA,BE=CG,進而得出△BEF≌△CGA,即可得出結論;
(2)同(1)的方法直接得出結論;
(3)同(1)的方法得出∠BEC=∠CGA,再用同弧所對的圓周角相等,進而得出△BFG∽△CAE,即可得出AE=kFG,進而用銳角三角函數和等腰三角形的性質得出FG,即可.
解答 解:(1)BF=AC,
理由:如圖1, 過點B,C,D作圓交AB于G,連接CG,
過點B,C,D作圓交AB于G,連接CG,
∴∠BGC=∠BDC,
∵∠BEC+∠BDC=180°,
∴∠BEC+∠BGC=180°,
∴∠BGC+∠AGC=180°,
∴∠BEC=∠CGA,
∵∠BEC+∠BDC=180°,∠BEC+∠AEC=180°,
∴∠BDC=∠AEC,
∵∠BDC=∠BGC,
∴∠CEG=∠CGE,
∴CE=CG,
∵CE=BE,
∴BE=CG,
在△BEF和△CGA中,$\left\{\begin{array}{l}{∠BEC=∠CGA}\\{BE=CG}\\{∠EBF=∠GCA(同弧所對的圓周角相等)}\end{array}\right.$,
∴△BEF≌△CGA,
∴BF=AC,
故答案為:BF;
(2)BF=AC仍然成立,
理由:同(1)的方法直接得出,BF=AC,
(3)如圖2, 過點B,C,D作圓交CF于G,連接BG,過點B作BM⊥CF,
過點B,C,D作圓交CF于G,連接BG,過點B作BM⊥CF,
∴∠BMF=90°,
∵點C,B,D,G四點共圓,
∵∠BEC+∠BDC=180°,∠BEC+∠BEF=180°,
∴∠BDC=∠BEF,
∵∠BGC=∠BDC,
∴∠BGE=∠BEG,
∴BG=BE,
∴∠BDC=∠BGC,
∵∠BEC+∠BDC=180°,
∴∠BEC+∠BGC=180°,
∵∠BGF+∠BGC=180°,
∴∠BGF=∠BEC,
∵∠FBG=∠DCF,
∴△BFG∽△CAE,
∴$\frac{FG}{AE}$=$\frac{BG}{CE}$,
∵BG=BE,
∴$\frac{FG}{AE}$=$\frac{BE}{CE}$,
∵CE=kBE,
∴$\frac{FG}{AE}$=$\frac{BE}{CE}$=$\frac{1}{k}$,
∴AE=kFG,
在Rt△BMF中,BF=m,∠BFE=α,
∴cosα=$\frac{FM}{BF}$,
∴FM=BF•cosα=m•cosα,
∵EF=n,
∴EF=FM+ME,
∴ME=EF-FM=n-m•cosα,
∵BG=BE,BM⊥CF,
∴EG=2ME=2(n-m•cosα),
∴FG=EF-EG=n-2(n-m•cosα),
∴AE=kFG=k[n-2(n-m•cosα)]=k(2m•cosα-n).
點評 此題是相似形綜合題,主要考查了全等三角形的判定和性質,圓周角的性質,相似三角形性質和判定,銳角三角函數,等腰三角形的性質,作出輔助線是解本題的關鍵,用類比的方法得出后面兩問是解本題的難點.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:初中數學 來源: 題型:填空題
 八年級(3)班開展了手工制作競賽,每個同學都在規定時間內完成一件手工作品.陳莉同學在制作手工作品的第一、二個步驟是:①先裁下了一張長BC=20cm,寬AB=16cm的矩形紙片ABCD,②將紙片沿著直線AE折疊,點D恰好落在BC邊上的F處,則EC的長為6 cm.
八年級(3)班開展了手工制作競賽,每個同學都在規定時間內完成一件手工作品.陳莉同學在制作手工作品的第一、二個步驟是:①先裁下了一張長BC=20cm,寬AB=16cm的矩形紙片ABCD,②將紙片沿著直線AE折疊,點D恰好落在BC邊上的F處,則EC的長為6 cm.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在△ABC中,AQ平分∠BAC,QD⊥BC交BC于點D,在BC上取一點E,使得∠BAD=∠CAE,在AE上存在一點K,使得∠KBC=2∠BQD,求證:QK平分∠BKC.
如圖,在△ABC中,AQ平分∠BAC,QD⊥BC交BC于點D,在BC上取一點E,使得∠BAD=∠CAE,在AE上存在一點K,使得∠KBC=2∠BQD,求證:QK平分∠BKC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知如圖,△ABC為等邊三角形,AB=6cm,D點在BC上,且∠ADE=60°,$\frac{DB}{DC}$=$\frac{1}{2}$,求AE的長.
已知如圖,△ABC為等邊三角形,AB=6cm,D點在BC上,且∠ADE=60°,$\frac{DB}{DC}$=$\frac{1}{2}$,求AE的長.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
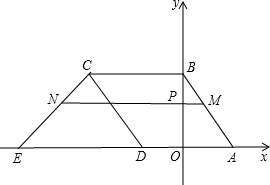 直線y=-$\frac{4}{3}$x+4與x軸交于點A,與y軸交于點B,菱形ABCD如圖放置在平面直角坐標系中,其中點D在x軸負半軸上,直線y=x+m經過點C,交x軸于點E.
直線y=-$\frac{4}{3}$x+4與x軸交于點A,與y軸交于點B,菱形ABCD如圖放置在平面直角坐標系中,其中點D在x軸負半軸上,直線y=x+m經過點C,交x軸于點E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com