
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 分別在邊
分別在邊![]() ,
,![]() 上,點(diǎn)
上,點(diǎn)![]() 分別在
分別在![]() ,
,![]() 上,
上,![]() ,
,![]() 交于點(diǎn)
交于點(diǎn)![]() ,記
,記![]() .
.
(1)若![]() 的值是1,當(dāng)
的值是1,當(dāng)![]() 時(shí),求
時(shí),求![]() 的值.
的值.
(2)若![]() 的值是
的值是![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
(3)若![]() 的值是3,當(dāng)點(diǎn)
的值是3,當(dāng)點(diǎn)![]() 是矩形的頂點(diǎn),
是矩形的頂點(diǎn),![]() ,
,![]() 時(shí),求
時(shí),求![]() 的值.
的值.
【答案】(1)![]() ;(2)最大值為
;(2)最大值為![]() ,最小值為
,最小值為![]() ;(3)
;(3)![]() 的值為
的值為![]() 或
或![]() .
.
【解析】
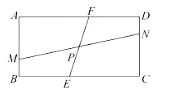
(1)作EH⊥BC于H,MQ⊥CD于Q,設(shè)EF交MN于點(diǎn)O.證明△FHE≌△MQN(ASA),即可解決問(wèn)題.
(2)由題意:2a≤MN≤![]() a,a≤EF≤
a,a≤EF≤![]() a,當(dāng)MN的長(zhǎng)取最大時(shí),EF取最短,此時(shí)k的值最大,最大值=
a,當(dāng)MN的長(zhǎng)取最大時(shí),EF取最短,此時(shí)k的值最大,最大值=![]() ,當(dāng)MN的最短時(shí),EF的值取最大,此時(shí)k的值最小,最小值為
,當(dāng)MN的最短時(shí),EF的值取最大,此時(shí)k的值最小,最小值為![]() .
.
(3)連接FN,ME.由k=3,MP=EF=3PE,推出![]() ,推出
,推出![]() ,由△PNF∽△PME,推出
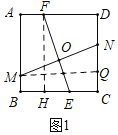
,由△PNF∽△PME,推出![]() =2,ME∥NF,設(shè)PE=2m,則PF=4m,MP=6m,NP=12m,接下來(lái)分兩種情形①如圖2中,當(dāng)點(diǎn)N與點(diǎn)D重合時(shí),點(diǎn)M恰好與B重合.②如圖3中,當(dāng)點(diǎn)N與C重合,分別求解即可.
=2,ME∥NF,設(shè)PE=2m,則PF=4m,MP=6m,NP=12m,接下來(lái)分兩種情形①如圖2中,當(dāng)點(diǎn)N與點(diǎn)D重合時(shí),點(diǎn)M恰好與B重合.②如圖3中,當(dāng)點(diǎn)N與C重合,分別求解即可.
(1)作![]() ,
,![]() ,如圖1.
,如圖1.
∵四邊形![]() 為正方形,
為正方形,
∴![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
(2)∵![]() ,∴
,∴![]() .
.
由題意得,![]() ,
,![]() ,
,
當(dāng)![]() 取最長(zhǎng)時(shí),
取最長(zhǎng)時(shí),![]() 可取到最短,此時(shí)
可取到最短,此時(shí)![]() 的值最大,最大值為
的值最大,最大值為![]() ,
,
當(dāng)![]() 取最短時(shí),
取最短時(shí),![]() 可取到最長(zhǎng),此時(shí)
可取到最長(zhǎng),此時(shí)![]() 的值最小,最小值為
的值最小,最小值為![]() .
.
(3)連結(jié)![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
設(shè)![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
①當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時(shí), 如圖2,點(diǎn)
重合時(shí), 如圖2,點(diǎn)![]() 恰好與點(diǎn)
恰好與點(diǎn)![]() 重合,過(guò)點(diǎn)
重合,過(guò)點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
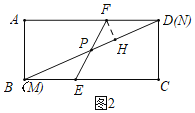
②當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時(shí),如圖3,過(guò)點(diǎn)
重合時(shí),如圖3,過(guò)點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,
,

則![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
綜上所述,![]() 的值為
的值為![]() 或
或![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
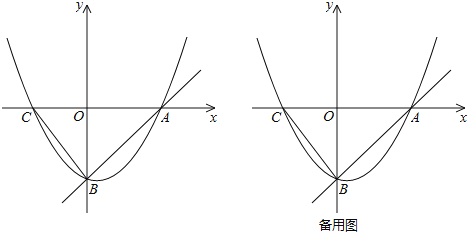
【題目】如圖,直線y=x﹣4與x軸、y軸分別交于A、B兩點(diǎn),拋物線y=![]() x2+bx+c經(jīng)過(guò)A、B兩點(diǎn),與x軸的另一個(gè)交點(diǎn)為C,連接BC.
x2+bx+c經(jīng)過(guò)A、B兩點(diǎn),與x軸的另一個(gè)交點(diǎn)為C,連接BC.
(1)求拋物線的解析式及點(diǎn)C的坐標(biāo);
(2)點(diǎn)M在拋物線上,連接MB,當(dāng)∠MBA+∠CBO=45°時(shí),求點(diǎn)M的坐標(biāo);
(3)點(diǎn)P從點(diǎn)C出發(fā),沿線段CA由C向A運(yùn)動(dòng),同時(shí)點(diǎn)Q從點(diǎn)B出發(fā),沿線段BC由B向C運(yùn)動(dòng),P、Q的運(yùn)動(dòng)速度都是每秒1個(gè)單位長(zhǎng)度,當(dāng)Q點(diǎn)到達(dá)C點(diǎn)時(shí),P、Q同時(shí)停止運(yùn)動(dòng),試問(wèn)在坐標(biāo)平面內(nèi)是否存在點(diǎn)D,使P、Q運(yùn)動(dòng)過(guò)程中的某一時(shí)刻,以C、D、P、Q為頂點(diǎn)的四邊形為菱形?若存在,直接寫(xiě)出點(diǎn)D的坐標(biāo);若不存在,說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,在矩形ABCD中,AB<BC,點(diǎn)E為對(duì)角線AC上的一個(gè)動(dòng)點(diǎn),連接BE,DE,過(guò)E作EF⊥BC于F.設(shè)AE=x,圖1中某條線段的長(zhǎng)為y,若表示y與x的函數(shù)關(guān)系的圖象大致如圖2所示,則這條線段可能是圖1中的( )

A.線段BEB.線段EFC.線段CED.線段DE
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
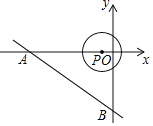
【題目】如圖,直線![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,交
,交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 軸上一動(dòng)點(diǎn),以點(diǎn)
軸上一動(dòng)點(diǎn),以點(diǎn)![]() 為圓心,以1個(gè)單位長(zhǎng)度為半徑作
為圓心,以1個(gè)單位長(zhǎng)度為半徑作![]() ,當(dāng)
,當(dāng)![]() 與直線
與直線![]() 相切時(shí),點(diǎn)
相切時(shí),點(diǎn)![]() 的坐標(biāo)是_____.
的坐標(biāo)是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】小明、小聰參加了![]() 跑的5期集訓(xùn),每期集訓(xùn)結(jié)束市進(jìn)行測(cè)試,根據(jù)他們的集訓(xùn)時(shí)間、測(cè)試成績(jī)繪制成如下兩個(gè)統(tǒng)計(jì)圖:
跑的5期集訓(xùn),每期集訓(xùn)結(jié)束市進(jìn)行測(cè)試,根據(jù)他們的集訓(xùn)時(shí)間、測(cè)試成績(jī)繪制成如下兩個(gè)統(tǒng)計(jì)圖:
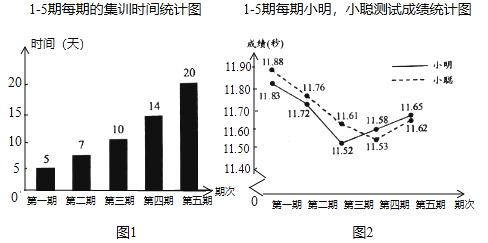
根據(jù)圖中信息,解答下列問(wèn)題:
(1)這5期的集訓(xùn)共有多少天?小聰5次測(cè)試的平均成績(jī)是多少?
(2)根據(jù)統(tǒng)計(jì)數(shù)據(jù),結(jié)合體育運(yùn)動(dòng)的實(shí)際,從集訓(xùn)時(shí)間和測(cè)試成績(jī)這兩方面,說(shuō)說(shuō)你的想法.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某學(xué)校為了解全校學(xué)生對(duì)電視節(jié)目的喜愛(ài)情況(新聞、體育、動(dòng)畫(huà)、娛樂(lè)、戲曲),從全校學(xué)生中隨機(jī)抽取部分學(xué)生進(jìn)行問(wèn)卷調(diào)查,并把調(diào)查結(jié)果繪制成兩幅不完整的統(tǒng)計(jì)圖.

請(qǐng)根據(jù)以上信息,解答下列問(wèn)題:
(1)這次被調(diào)查的學(xué)生共有多少人?
(2)請(qǐng)將條形統(tǒng)計(jì)圖補(bǔ)充完整;
(3)若該校約有1500名學(xué)生,估計(jì)全校學(xué)生中喜歡娛樂(lè)節(jié)目的有多少人?
(4)該校廣播站需要廣播員,現(xiàn)決定從喜歡新聞節(jié)目的甲、乙、丙、丁四名同學(xué)中選取2名,求恰好選中甲、乙兩位同學(xué)的概率(用樹(shù)狀圖或列表法解答)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為增強(qiáng)學(xué)生環(huán)保意識(shí),某中學(xué)舉辦了環(huán)保知識(shí)競(jìng)賽,某班共有5名學(xué)生(3名男生,2名女生)獲獎(jiǎng).
(1)老師若從獲獎(jiǎng)的5名學(xué)生中選取一名作為班級(jí)的“環(huán)保小衛(wèi)士”,則恰好是男生的概率為 .
(2)老師若從獲獎(jiǎng)的5名學(xué)生中任選兩名作為班級(jí)的“環(huán)保小衛(wèi)士”,請(qǐng)用畫(huà)樹(shù)狀圖法或列表法,求出恰好是一名男生、一名女生的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】隨著互聯(lián)網(wǎng)、移動(dòng)終端的迅速發(fā)展,數(shù)字化閱讀越來(lái)越普及,公交、地鐵上的“低頭族”越來(lái)越多.某研究機(jī)構(gòu)針對(duì)“您如何看待數(shù)字化閱讀”問(wèn)題進(jìn)行了隨機(jī)問(wèn)卷調(diào)查(問(wèn)卷調(diào)查表如下圖所示),并將調(diào)查結(jié)果繪制成圖1和圖2所示的統(tǒng)計(jì)圖(均不完整).請(qǐng)根據(jù)統(tǒng)計(jì)圖中提供的信息,解答下列問(wèn)題:

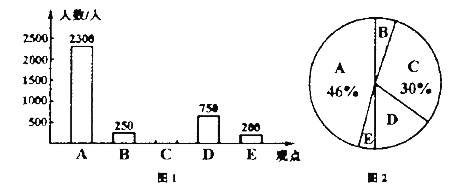
(1)本次接受調(diào)查的共有多少人?
(2)在接受調(diào)查的人當(dāng)中,請(qǐng)求出選擇“觀點(diǎn)![]() ”的人數(shù),并將條形統(tǒng)計(jì)圖補(bǔ)充完整;
”的人數(shù),并將條形統(tǒng)計(jì)圖補(bǔ)充完整;
(3)在扇形統(tǒng)計(jì)圖中,“觀點(diǎn)![]() ”對(duì)應(yīng)的圓心角為多少度?
”對(duì)應(yīng)的圓心角為多少度?
(4)現(xiàn)在你是該研究機(jī)構(gòu)的研究員,根據(jù)以上調(diào)查結(jié)果,你分別從選擇“觀點(diǎn)![]() 、觀點(diǎn)
、觀點(diǎn)![]() 、觀點(diǎn)
、觀點(diǎn)![]() 、觀點(diǎn)
、觀點(diǎn)![]() 的調(diào)查人員中,每項(xiàng)隨機(jī)抽取1人,再?gòu)倪@4人中,任選2人進(jìn)行個(gè)別座談,請(qǐng)用列表法成樹(shù)狀圖法求選取的兩人恰好是選擇“觀點(diǎn)
的調(diào)查人員中,每項(xiàng)隨機(jī)抽取1人,再?gòu)倪@4人中,任選2人進(jìn)行個(gè)別座談,請(qǐng)用列表法成樹(shù)狀圖法求選取的兩人恰好是選擇“觀點(diǎn)![]() 、觀點(diǎn)
、觀點(diǎn)![]() ”的概率.
”的概率.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com