
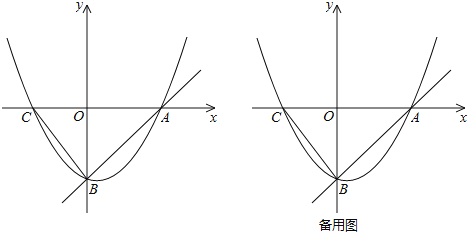
���}Ŀ����D��ֱ��y��x��4�cx�S��y�S�քe����A��B���c(di��n)�����タy��![]() x2+bx+c��(j��ng)�^A��B���c(di��n)���cx�S����һ�����c(di��n)��C���B��BC��
x2+bx+c��(j��ng)�^A��B���c(di��n)���cx�S����һ�����c(di��n)��C���B��BC��
��1�����タ�Ľ���ʽ���c(di��n)C������(bi��o)��
��2���c(di��n)M�ڒ��タ�ϣ��B��MB����(d��ng)��MBA+��CBO��45��r�����c(di��n)M������(bi��o)��
��3���c(di��n)P���c(di��n)C���l(f��)���ؾ���CA��C��A�\(y��n)�ӣ�ͬ�r�c(di��n)Q���c(di��n)B���l(f��)���ؾ���BC��B��C�\(y��n)�ӣ�P��Q���\(y��n)���ٶȶ���ÿ��1����λ�L�ȣ���(d��ng)Q�c(di��n)���_(d��)C�c(di��n)�r��P��Qͬ�rֹͣ�\(y��n)�ӣ�ԇ��������(bi��o)ƽ���(n��i)�Ƿ�����c(di��n)D��ʹP��Q�\(y��n)���^���е�ijһ�r�̣���C��D��P��Q����c(di��n)����߅�Ξ����Σ������ڣ�ֱ�ӌ����c(di��n)D������(bi��o)���������ڣ��f�����ɣ�
���𰸡���1��y��![]() x2��
x2��![]() x��4��C����3��0������2���M��l�����c(di��n)M������(bi��o)�飨
x��4��C����3��0������2���M��l�����c(di��n)M������(bi��o)�飨![]() ����
����![]() ����5��
����5��![]() ������3�����ڝM��l�����c(di��n)D���c(di��n)D����(bi��o)�飨��
������3�����ڝM��l�����c(di��n)D���c(di��n)D����(bi��o)�飨��![]() ����
����![]() ����1����2����
����1����2����![]() ��
��![]() ����
����
��������
��һ�������ʽ��Ҫ���ô���ϵ��(sh��)��⣬����һ�κ���(sh��)y��x��4������A�c(di��n)����(bi��o)��B�c(di��n)����(bi��o)��Ȼ����뷽�̼��ɣ�
�ڶ������M�c(di��n)������(bi��o)����ҪӑՓ����?y��n)?/span>��MBA+��CBO��45���DŽӑB(t��i)�ģ��ʮ�(d��ng)BM��BC�r��һ�N��r������tan��M1BE��tan��BCO��![]() �����Խo����ʽ�P(gu��n)ϵ�����M�c(di��n)��BM�cBC�P(gu��n)��y�S���Q�r�ǵڶ��N��r��tan��M2BE��tan��CBO��
�����Խo����ʽ�P(gu��n)ϵ�����M�c(di��n)��BM�cBC�P(gu��n)��y�S���Q�r�ǵڶ��N��r��tan��M2BE��tan��CBO��![]() �����Գ��o��ʽ�P(gu��n)ϵ�����M�c(di��n)
�����Գ��o��ʽ�P(gu��n)ϵ�����M�c(di��n)
����������ҪӑՓ����?y��n)��Ă��c(di��n)��֪�����������c(di��n)�������@��ӑՓ����(d��ng)CP�����ε�߅��CQ�錦�Ǿ��@�ǵ�һ�N��r�����ý�ֱ�����������Q�c(di��n)�Ŀv����(bi��o)����֪��D�c(di��n)�Ŀv����(bi��o)��Ȼ������cos��BCO��![]() ��������ʽ����������ε�߅�L����������߅�L��Q�c(di��n)�M����(bi��o)�����ɵõ�Q�c(di��n)�M����(bi��o)����(d��ng)CQ��CP�������ε�߅�@�ǵڶ��N��r����?y��n)?/span>CP=CQ=BQ������Q�c(di��n)��BC���У������ε�߅�L�����ˣ����ý�ֱ�������μ��ɽo��Q�c(di��n)�Ŀv����(bi��o)��֪�����ε�߅�L������D�c(di��n)�ęM�v����(bi��o)�������ˣ���(d��ng)CQ�����ε�߅��CP�����εČ��Ǿ��@�ǵ����N��r�����ý�ֱ�������Σ����Խo��Q�c(di��n)����(bi��o)���҂�����֪��D�c(di��n)��Q�c(di��n)�P(gu��n)��x�S���Q�������εĻ������|(zh��)����֪��������D�c(di��n)����(bi��o)������
��������ʽ����������ε�߅�L����������߅�L��Q�c(di��n)�M����(bi��o)�����ɵõ�Q�c(di��n)�M����(bi��o)����(d��ng)CQ��CP�������ε�߅�@�ǵڶ��N��r����?y��n)?/span>CP=CQ=BQ������Q�c(di��n)��BC���У������ε�߅�L�����ˣ����ý�ֱ�������μ��ɽo��Q�c(di��n)�Ŀv����(bi��o)��֪�����ε�߅�L������D�c(di��n)�ęM�v����(bi��o)�������ˣ���(d��ng)CQ�����ε�߅��CP�����εČ��Ǿ��@�ǵ����N��r�����ý�ֱ�������Σ����Խo��Q�c(di��n)����(bi��o)���҂�����֪��D�c(di��n)��Q�c(di��n)�P(gu��n)��x�S���Q�������εĻ������|(zh��)����֪��������D�c(di��n)����(bi��o)������
��1��ֱ������ʽy��x��4��
��x��0����y����4��
��y��0����x��4��
��A��4��0����B��0����4����
���c(di��n)A��B�ڒ��タy��![]() x2+bx+c�ϣ�
x2+bx+c�ϣ�
��
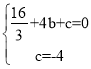 ��
��
���![]() ��
��
�����タ����ʽ�飺y��![]() x2��
x2��![]() x��4��
x��4��
��y��![]() x2��
x2��![]() x��4��0��
x��4��0��
��ã�x����3��x��4��
��C����3��0����
��2����MBA+��CBO��45�㣬
�O(sh��)M��x��y����
����(d��ng)BM��BC�r������D2��1��ʾ��
�ߡ�ABO��45�㣬
���MBA+��CBO��45�㣬���c(di��n)M�M��l����
�^�c(di��n)M1��M1E��y�S���c(di��n)E���tM1E��x��OE����y��
��BE��4+y��
��tan��M1BE��tan��BCO��![]() ��
��
��![]() ��
��
��ֱ��BM1�Ľ���ʽ�飺y��![]() x��4��
x��4��
(li��n)��y��![]() x��4�cy��
x��4�cy��![]() x2��
x2��![]() x��4��
x��4��
�ã�![]() x��4��
x��4��![]() x2��
x2��![]() x��4��
x��4��
��ã�x1��0��x2��![]() ��
��
��y1����4��y2����![]() ��
��
��M1��![]() ����
����![]() ����
����
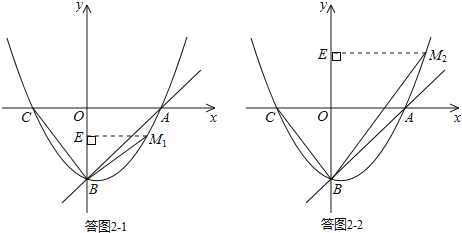
����(d��ng)BM�cBC�P(gu��n)��y�S���Q�r������D2��2��ʾ��
�ߡ�ABO����MBA+��MBO��45�㣬��MBO����CBO��
���MBA+��CBO��45�㣬
���c(di��n)M�M��l����
�^�c(di��n)M2��M2E��y�S���c(di��n)E��
�tM2E��x��OE��y��
��BE��4+y��
��tan��M2BE��tan��CBO��![]() ��
��
��![]() ��
��
��ֱ��BM2�Ľ���ʽ�飺y��![]() x��4��
x��4��
(li��n)��y��![]() x��4�cy��
x��4�cy��![]() x2��
x2��![]() x��4�ã�
x��4�ã�![]() x��4��
x��4��![]() x2��
x2��![]() x��4��
x��4��
��ã�x1��0��x2��5��
��y1����4��y2��![]() ��
��
��M2��5��![]() ����
����
�C���������M��l�����c(di��n)M������(bi��o)�飺��![]() ����
����![]() ����5��
����5��![]() ����
����
��3���O(sh��)��BCO�������ttan����![]() ��sin����
��sin����![]() ��cos����
��cos����![]() ��
��
���O(sh��)���ڝM��l�����c(di��n)D���O(sh��)���εČ��Ǿ������c(di��n)E���O(sh��)�\(y��n)�ӕr�g��t��
������CQ�����Ό��Ǿ�������D3��1���˕rBQ��t������߅�L��t��
��CE��![]() CQ��
CQ��![]() ��5��t����
��5��t����
��Rt��PCE��cos����![]() ��
��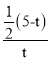 ��
��![]() ��
��
���t��![]() ��
��
��CQ��5��t��![]() ��
��
�^�c(di��n)Q��QF��x�S���c(di��n)F��
�tQF��CQsin����![]() ��CF��CQcos����
��CF��CQcos����![]() ��
��
��OF��3��CF��![]() ��
��
��Q����![]() ����
����![]() ����
����
���c(di��n)D1�c�c(di��n)Q�M����(bi��o)���t�����
��D1����![]() ����
����![]() ����
����
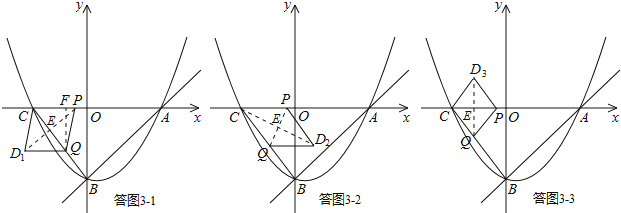
������PQ�����Ό��Ǿ�������D3��2���˕rBQ��t������߅�L��t��
��BQ��CQ��t��
��t��![]() ���c(di��n)Q��BC���c(di��n)��
���c(di��n)Q��BC���c(di��n)��
��Q����![]() ����2����
����2����
���c(di��n)D2�c�c(di��n)Q�M����(bi��o)���t�����
��D2��1����2����
������CP�����Ό��Ǿ�������D3��3���˕rBQ��t������߅�L��5��t��
��Rt��CEQ��cos����![]() ��
��![]() ��
��![]() ��
��
���t��![]() ��
��
��OE��3��CE��3��![]() t��
t��![]() ��D3E��QE��CQsin������5��
��D3E��QE��CQsin������5��![]() ����
����![]() ��
��![]() ��
��
��D3����![]() ��
��![]() ����
����
�C�����������ڝM��l�����c(di��n)D���c(di��n)D����(bi��o)�飺����![]() ����
����![]() ����1����2����
����1����2����![]() ��
��![]() ����
����


 �옷5��2���ϵ�д�
�옷5��2���ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
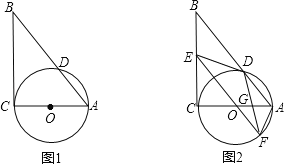
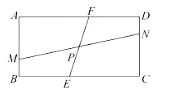
���}Ŀ����D����Rt��ABC�У���C��90�㣬��AC��ֱ������O����AB��D��
(1)�ڈD(1)�У���ֱ�ߺ͈AҎ(gu��)�^�c(di��n)D����O���о�DE��BC���c(di��n)E��(�������D���E����������)
(2)��D(2)�������O�İ돽��3��ED��4�����LEO����O��F���B��DF���cOA�����c(di��n)G����OG���L��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���κ���(sh��)![]() �ĈD����D��ʾ�������½Y(ji��)Փ����
�ĈD����D��ʾ�������½Y(ji��)Փ����![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() �����������_�Y(ji��)Փ����̖�ǣ� ��
�����������_�Y(ji��)Փ����̖�ǣ� ��

A. �٢� B. �٢ۢ� C. �٢ڢۢ� D. �٢ڢۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
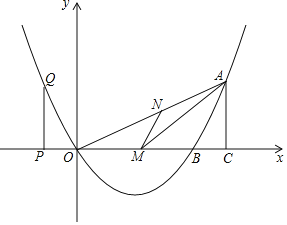
���}Ŀ����D����֪���κ���(sh��)�ĈD���^�c(di��n)O��0��0����A��8��4�����cx�S������һ�c(di��n)B���Ҍ��Q�S��ֱ��x��3��
��1����ԓ���κ���(sh��)�Ľ���ʽ��
��2����M��OB�ϵ�һ�c(di��n)����MN��AB��OA��N����(d��ng)��ANM��e���r����M������(bi��o)��
��3��P��x�S�ϵ��c(di��n)���^P��PQ��x�S�c���タ����Q���^A��AC��x�S��C����(d��ng)��O��P��Q����c(di��n)���������c��O��A��C����c(di��n)�����������ƕr����P�c(di��n)������(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�W(xu��)У�����˽ⱾУ1200���W(xu��)�����n����x����r���F(xi��n)�ĸ��꼉�S�C(j��)��ȡ�˲��W(xu��)��������һ�ܵ��n����x�r�g�M(j��n)�����{(di��o)�飬���L�Ƴ����µĽy(t��ng)Ӌ�D���͈D��������(j��)���P(gu��n)��Ϣ��������І��}��
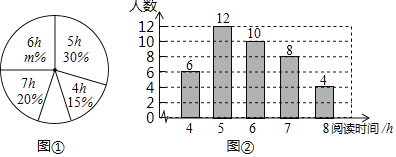
��1�����ν����S�C(j��)����{(di��o)��ČW(xu��)���˔�(sh��)���� �D����m��ֵ���� ��
��2�������{(di��o)��@ȡ�Ęӱ���(sh��)��(j��)�ı���(sh��)���� ����λ��(sh��)���� ��
��3�����{(di��o)��@ȡ�Ęӱ���(sh��)��(j��)ƽ����(sh��)��
��4������(j��)�ӱ���(sh��)��(j��)����ӋԓУһ�ܵ��n����x�r�g����6h�ČW(xu��)���˔�(sh��)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������С�}�M��10�֣���D����Rt��ABC�У���ABC=90����AC�Ĵ�ֱƽ�־��քe�cAC��BC��AB�����L���ཻ���c(di��n)D��E��F����BF=BC����O����BEF����ӈA����EBF��ƽ�־���EF���c(di��n)G�������c(di��n)H���B��BD��FH��
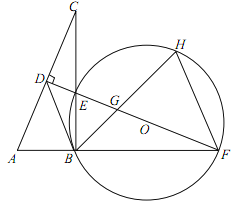
��1�����C����ABC�ա�EBF��
��2��ԇ�Д�BD�c��O��λ���P(gu��n)ϵ�����f�����ɣ�
��3����AB=1����HGHB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
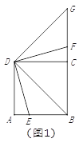
���}Ŀ������D1��![]() ��������
��������![]() ߅
߅![]() �ϵ�һ�c(di��n)���B��
�ϵ�һ�c(di��n)���B��![]() ����
����![]() �@���c(di��n)
�@���c(di��n)![]() ��r����D(zhu��n)90�������D(zhu��n)��ǵă�߅�քe�c�侀
��r����D(zhu��n)90�������D(zhu��n)��ǵă�߅�քe�c�侀![]() �����c(di��n)
�����c(di��n)![]() ���c(di��n)
���c(di��n)![]() .
.
�پ���![]() ��
��![]() �Ĕ�(sh��)���P(gu��n)ϵ�� ��
�Ĕ�(sh��)���P(gu��n)ϵ�� ��
�ڌ�������![]() ��
��![]() ֮�g�Ĕ�(sh��)���P(gu��n)ϵ.
֮�g�Ĕ�(sh��)���P(gu��n)ϵ.
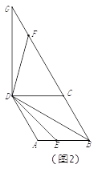
�Ʈ�(d��ng)��߅��![]() �����Σ�
������![]() ���c(di��n)
���c(di��n)![]() ������
������![]() ߅
߅![]() ����ֱ���ϵ�һ�c(di��n)���B��
����ֱ���ϵ�һ�c(di��n)���B��![]() ����
����![]() �@���c(di��n)
�@���c(di��n)![]() ��r����D(zhu��n)120�������D(zhu��n)��ǵă�߅�քe�c�侀
��r����D(zhu��n)120�������D(zhu��n)��ǵă�߅�քe�c�侀![]() �����c(di��n)
�����c(di��n)![]() ���c(di��n)
���c(di��n)![]() .
.
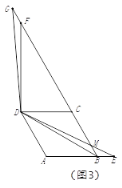
����D2���c(di��n)![]() �ھ����ϕr��Ո?zh��)�������
�ھ����ϕr��Ո?zh��)�������![]() ��
��![]() ֮�g�Ĕ�(sh��)���P(gu��n)ϵ�������Y(ji��)Փ���o���C����
֮�g�Ĕ�(sh��)���P(gu��n)ϵ�������Y(ji��)Փ���o���C����
����D3���c(di��n)![]() �ھ���
�ھ���![]() �����L���ϕr��
�����L���ϕr��![]() ���侀
���侀![]() ���c(di��n)
���c(di��n)![]() ����
���� ![]() ,ֱ�ӌ�������
,ֱ�ӌ�������![]() ���L��.
���L��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����߅��ABCD�����Σ����Ǿ�AC��BD�ཻ���c(di��n)O��DH��AB���c(di��n)H���B��OH������DHO��20�㣬�t��ADC�ĶȔ�(sh��)�ǣ�������
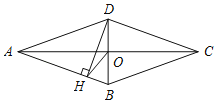
A. 120��B. 130��C. 140��D. 150��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D������![]() �У�
��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() �քe��߅
�քe��߅![]() ��
��![]() �ϣ��c(di��n)
�ϣ��c(di��n)![]() �քe��
�քe��![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() �����c(di��n)
�����c(di��n)![]() ��ӛ
��ӛ![]() .
.
��1����![]() ��ֵ��1����(d��ng)
��ֵ��1����(d��ng)![]() �r����
�r����![]() ��ֵ.
��ֵ.
��2����![]() ��ֵ��
��ֵ��![]() ����
����![]() �����ֵ����Сֵ.
�����ֵ����Сֵ.
��3����![]() ��ֵ��3����(d��ng)�c(di��n)
��ֵ��3����(d��ng)�c(di��n)![]() �Ǿ��ε���c(di��n)��
�Ǿ��ε���c(di��n)��![]() ��
��![]() �r����
�r����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com