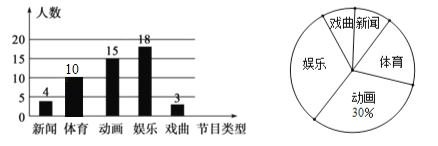
【題目】某學校為了解全校學生對電視節目的喜愛情況(新聞、體育、動畫、娛樂、戲曲),從全校學生中隨機抽取部分學生進行問卷調查，并把調查結果繪制成兩幅不完整的統計圖.
請根據以上信息,解答下列問題:
(1)這次被調查的學生共有多少人?
(2)請將條形統計圖補充完整;
(3)若該校約有1500名學生,估計全校學生中喜歡娛樂節目的有多少人?
(4)該校廣播站需要廣播員,現決定從喜歡新聞節目的甲、乙、丙、丁四名同學中選取2名,求恰好選中甲、乙兩位同學的概率(用樹狀圖或列表法解答)
【答案】（1）50人；（2）補圖見解析；（3）540人；（4）
【解析】（1）根據動畫類人數及其百分比求得總人數；
（2）總人數減去其他類型人數可得體育類人數，據此補全圖形即可；
（2）用樣本估計總體的思想解決問題；
（3）根據題意先畫出樹狀圖，得出所有情況數，再根據概率公式即可得出答案．
（1）這次被調查的學生人數為15÷30%=50人；
（2）喜愛“體育”的人數為50﹣（4+15+18+3）=10人，補全圖形如下：
（3）估計全校學生中喜歡娛樂節目的有1500×
=540人；
（4）列表如下：
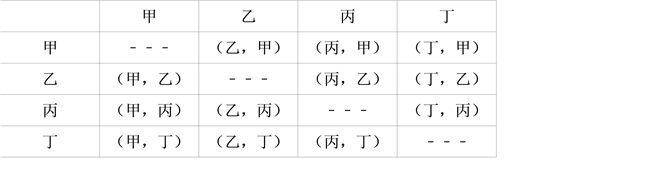
所有等可能的結果為12種，恰好選中甲、乙兩位同學的有2種結果，所以恰好選中甲、乙兩位同學的概率為
=．
新非凡教輔沖刺100分系列答案科目：初中數學 來源： 題型：
【題目】如圖，以線段AB為直徑作⊙O，CD與⊙O相切于點E，交AB的延長線于點D， 連接BE，過點O作OC∥BE交切線DE于點C，連接AC ．
（1）求證：AC是⊙O的切線 ；
（2）若BD=OB=4，求弦AE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】問題情境
在綜合與實踐課上，老師讓同學們以“兩條平行線AB，CD和一塊含60°角的直角三角尺EFG(∠EFG＝90°，∠EGF＝60°)”為主題開展數學活動．
操作發現
(1)如圖(1)，小明把三角尺的60°角的頂點G放在CD上，若∠2＝2∠1，求∠1的度數；
(2)如圖(2)，小穎把三角尺的兩個銳角的頂點E、G分別放在AB和CD上，請你探索并說明∠AEF與∠FGC之間的數量關系；
結論應用
(3)如圖(3)，小亮把三角尺的直角頂點F放在CD上，30°角的頂點E落在AB上．若∠AEG＝α，則∠CFG等于______(用含α的式子表示)．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用同樣規格的黑、白兩種顏色的正方形瓷磚按下圖所示的方式鋪寬為1.5米的小路.
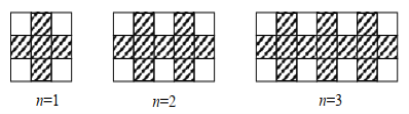
（1）鋪第5個圖形用黑色正方形瓷磚 塊；
（2）按照此方式鋪下去，鋪第 n 個圖形用黑色正方形瓷磚 塊；（用含 n的代數式表示）
（3）若黑、白兩種顏色的瓷磚規格都為（ 長0.5米寬0.5米），且黑色正方形瓷磚每塊價格 25 元，白色正方形瓷磚每塊價格30元，若按照此方式恰好鋪滿該小路某一段（該段小路的總面積為 18.75 平方米），求該段小路所需瓷磚的總費用．
查看答案和解析>>
科目：初中數學 來源： 題型：
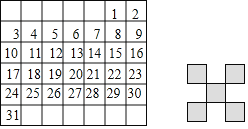
【題目】如圖是某月的月歷，用如圖恰好能完全遮蓋住月歷表中的五個數字，設帶陰影的“
”形中的5個數字的最小數為a．
請用含a的代數式表示這5個數；
這五個數的和與“”形中心的數有什么關系？
蓋住的5個數字的和能為105嗎？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面材料．
在數學課上，老師請同學思考如下問題：
已知：如圖①，在△ABC中，∠A＝90°.
圖①
求作：⊙P，使得點P在邊AC上，且⊙P與AB，BC都相切．
小軒的主要作法如下：
如圖②，
圖②
(1)作∠ABC的平分線BF，與AC交于點P；
(2)以P為圓心，AP長為半徑作⊙P，則⊙P即為所求．
老師說：“小軒的作法正確．”
請回答：⊙P與BC相切的依據是 ____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知：∠BAC的平分線與BC的垂直平分線DG相交于點D，DE⊥AB，DF⊥AC，垂足分別為E、F，AB=6，AC=3，則BE=_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，有一個水池，其底面是邊長為16尺的正方形，一根蘆葦AB生長在它的正中央，高出水面部分BC的長為2尺，如果把該蘆葦沿與水池邊垂直的方向拉向岸邊，那么蘆葦的頂部B恰好碰到岸邊的B′，則這根蘆葦AB的長是（ ）
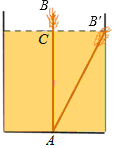
A. 15尺B. 16尺C. 17尺D. 18尺
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
