
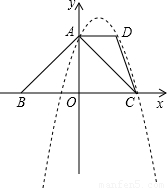
 ,即為半徑;
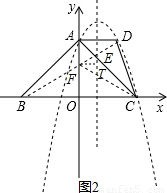
,即為半徑;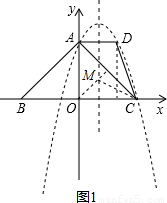 解:(1)由題意知C(3,0)、A(0,3).
解:(1)由題意知C(3,0)、A(0,3). ,即半徑為
,即半徑為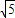 .
.
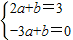 ,
,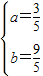 ,
, x+
x+ ,
, ,根據對稱軸為直線x=1,則y=2,
,根據對稱軸為直線x=1,則y=2, )、E(1,2),
)、E(1,2),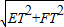 =
=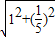 =
=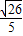 .
.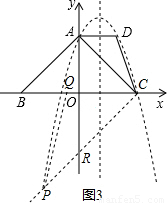
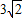 ,DC=
,DC=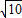 .
.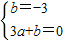 ,
,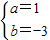 ,
, =5
=5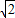 .
.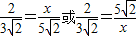 ,
,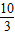 或x=15.
或x=15.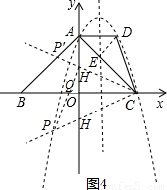
 ,0)或(-12,0).
,0)或(-12,0). =
=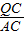 ,
,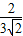 =
=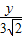 ,或
,或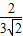 =
=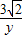 ,
,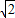 ,EC=2
,EC=2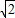 ,
,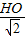 =
=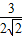 ,
, .
. x-
x- .
.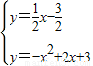 ,
, ,-
,- ),PC=
),PC=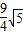 .
.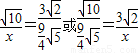 ,
,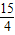 或x=
或x= ,
, ,0)或(-
,0)或(-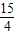 ,0).
,0). x+
x+ .
. ,
, ),
),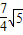 .
. ,
,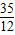 或
或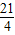 ,所以Q(
,所以Q(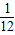 ,0)或(-
,0)或(- ,0).
,0). ,0)或(-12,0);P2(0,3)、Q2(1,0)或(-6,0);P3(-
,0)或(-12,0);P2(0,3)、Q2(1,0)或(-6,0);P3(- ,-
,- )、Q3(-
)、Q3(- ,0)或(-
,0)或(-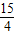 ,0);P4(-
,0);P4(- ,
, )、Q4(
)、Q4(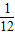 ,0)或(-
,0)或(- ,0).
,0).

 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:
 如圖,在梯形ABCD中,AB∥CD,E是AB邊上的點,給出下面三個論斷:①AD=BC;②DE=CE;③AE=BE.請你以其中的兩個論斷為條件,填入“已知”欄中,以一個論斷作為結論,填入“求證”欄中,使之成為一個正確的命題,并證明之.
如圖,在梯形ABCD中,AB∥CD,E是AB邊上的點,給出下面三個論斷:①AD=BC;②DE=CE;③AE=BE.請你以其中的兩個論斷為條件,填入“已知”欄中,以一個論斷作為結論,填入“求證”欄中,使之成為一個正確的命題,并證明之.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在梯形ABCD中,AD∥BC,AD=AB,過點A作AE∥DB交CB的延長線于點E.
如圖,在梯形ABCD中,AD∥BC,AD=AB,過點A作AE∥DB交CB的延長線于點E.查看答案和解析>>
科目:初中數學 來源: 題型:
| 8 |
| 5 |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com