科目：初中數學 來源： 題型：
如圖，拋物線C1：y=（x+m）2（m為常數，m＞0），平移拋物線y=﹣x2，使其頂點D在拋物線C1位于y軸右側的圖象上，得到拋物線C2．拋物線C2交x軸于A，B兩點（點A在點B的左側），交y軸于點C，設點D的橫坐標為a．
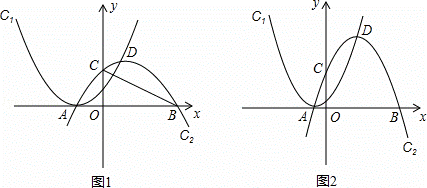
（1）如圖1，若m=．
①當OC=2時，求拋物線C2的解析式；
②是否存在a，使得線段BC上有一點P，滿足點B與點C到直線O
P的距離之和最大且AP=BP？若存在，求出a的值；若不存在，請說明理由；
（2）如圖2，當OB=2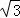
﹣m（0＜m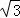＜）時，請直接寫出到△ABD的三邊所在直線的距離相等的所有點的坐標（用含m的式子表示）．
查看答案和解析>>
科目：初中數學 來源： 題型：
已知二次函數y=﹣x2+2bx+c，當x＞1時，y的值隨x值的增大而減小，則實數b的取值范圍是（ ）
|
| A． | b≥﹣1 | B． | b≤﹣1 | C． | b≥1 | D． | b≤1 |
查看答案和解析>>
科目：初中數學 來源： 題型：
湘西盛產椪柑，春節期間，一外地運銷客戶安排15輛汽車裝運A、B、C三種不同品質的椪柑120噸到外地銷售，按計劃15輛汽車都要裝滿且每輛汽車只能裝同一種品質的椪柑，每種椪柑所用車輛部不少于3輛．
（1）設裝運A種椪柑的車輛數為x輛，裝運B種椪柑車輛數為y輛，根據下表提供的信息，求出y與x之間的函數關系式；
| 椪柑品種 | A | B | C |
| 每輛汽車運載量 | 10 | 8 | 6 |
| 每噸椪柑獲利（元） | 800 | 1200 | 1000 |
（2）在（1）條件下，求出該函數自變量x的取值范圍，車輛的安排方案共有幾種？請寫出每種安排方案；
（3）為了減少椪柑積壓，湘西州制定出臺了促進椪柑銷售的優惠政策，在外地運銷客戶原有獲利不變的情況下，政府對外地運銷客戶，按每噸50元的標準實行運費補貼．若要使該外地運銷客戶所獲利潤W（元）最大，應采用哪種車輛安排方案？并求出利潤W（元）的最大值？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的解集是（ ）
≥
，并把它的解集在數軸上表示出來．
線段B0、0A勻速運動到點A，則0P的長度y與運動時間t之間的函數圖象大致是（ ）
