
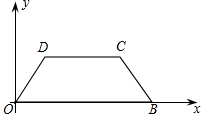
 OD=BC=2,CD=3.
OD=BC=2,CD=3. ?
?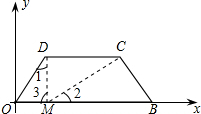 解:(1)如圖,從D點往OB坐垂線DM,由圖形可得OM=1,根據直角三角形性質可得出∠1=30°
解:(1)如圖,從D點往OB坐垂線DM,由圖形可得OM=1,根據直角三角形性質可得出∠1=30°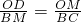
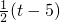 ,MN=
,MN=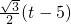
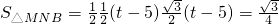 ,
,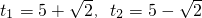 (不合,舍去)
(不合,舍去)
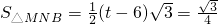
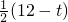 ,MN=
,MN=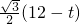 ,
,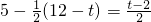
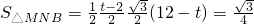
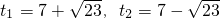 (不合,舍去)
(不合,舍去)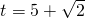 或
或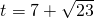 時,
時,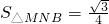 .
.


 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案科目:初中數學 來源: 題型:
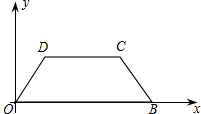 OD=BC=2,CD=3.
OD=BC=2,CD=3.
| ||
| 4 |
查看答案和解析>>
科目:初中數學 來源:2010-2011學年福建省泉州市德化縣(德化六中、蓋德中學、赤水中學)三校聯考九年級(上)期中數學試卷(解析版) 題型:解答題
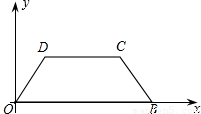
 ?
?
查看答案和解析>>
科目:初中數學 來源:2009-2010學年福建省泉州市南安市九年級(上)期末數學試卷(解析版) 題型:解答題
 ?
?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com