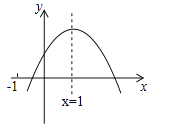
【題目】已知二次函數
的圖象如圖所示，有以下結論：
①abc＞0，
②a﹣b+c＜0，
③2a=b，
④4a+2b+c＞0，
⑤若點（﹣2，
）和（
，
）在該圖象上，則
．
其中正確的結論是 （填入正確結論的序號）．
科目：初中數學 來源： 題型：
【題目】閱讀理解在數軸上，
表示一個點在平面直角坐標系中，表示一條直線，如圖（a）所示在數軸上，
表示一條射線；在平面直角坐標系中，表示的是直線及右側的區域；在平面直角坐標系中，
表示經過
，
兩點的一條直線在平面直線坐標系中，
表示的是直線及下方的區域如圖（b）所示，
則表示的是直線及上方的區域如果x，y滿足
，請在圖（c）中用陰影描出點
所在的區域．
查看答案和解析>>
科目：初中數學 來源： 題型：
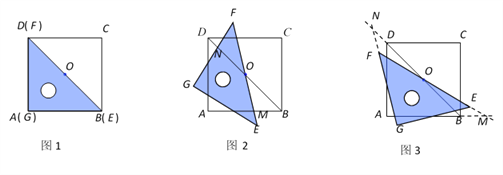
【題目】如圖1，一等腰直角三角尺GEF的兩條直角邊與正方形ABCD的兩條邊分別重合在一起．現正方形ABCD保持不動，將三角尺GEF繞斜邊EF的中點O（點O也是BD中點）按順時針方向旋轉．
（1）如圖2，當EF與AB相交于點M，GF與BD相交于點N時，通過觀察或測量BM，FN的長度，猜想BM，FN滿足的數量關系，并證明你的猜想；
（2）若三角尺GEF旋轉到如圖3所示的位置時，線段FE的延長線與AB的延長線相交于點M，線段BD的延長線與GF的延長線相交于點N，此時，（1）中的猜想還成立嗎？若成立，請證明；若不成立，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若點O是等腰△ABC的外心，且∠BOC＝60°，底邊BC＝2，則△ABC的面積為( )
A. 2＋
B. 
C. 2＋或2－ D. 4＋2或2－
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】y=ax2+bx+c的圖象與x軸交于A，B兩點，與y軸交于點C，當△ABC為直角三角形時，則（ ）
A. ac=﹣1 B. ac=1 C. ac=±1 D. 無法確定
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1所示，在△ABC中，AB的垂直平分線交BC于點M，交AB于點E，AC的垂直平分線交BC于點N，交AC于點F，連接AM、AN．
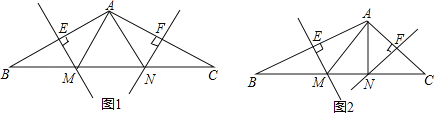
（1）求證：△AMN的周長＝BC；
（2）若AB＝AC，∠BAC＝120°，試判斷△AMN的形狀，并證明你的結論；
（3）若∠C＝45°，AC＝3
，BC＝9，如圖2所示，求MN的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合與探究
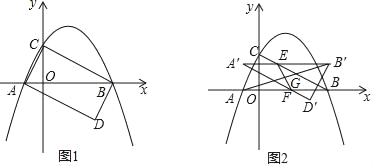
如圖1，拋物線y=ax2+bx+2與x軸交于A（﹣1，0），B（4，0）兩點，與y軸交于點C，連接AC，BC．D為坐標平面第四象限內一點，且使得△ABD與△ABC全等．
（1）求拋物線的表達式．
（2）請直接寫出點D的坐標，并判斷四邊形ACBD的形狀．
（3）如圖2，將△ABD沿y軸的正方形以每秒1個單位長度的速度平移，得到△A′B′D′，A′B′與BC交于點E，A′D′與AB交于點F．連接EF，AB′，EF與AB′交于點G．設運動的時間為t（0≤t≤2）秒．
①當直線EF經過拋物線的頂點T時，請求出此時t的值；
②請直接寫出點G經過的路徑的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
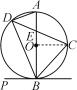
【題目】如圖：C、D是以AB為直徑的⊙O上的點，
，弦CD交AB于點E.
（1）當PB是⊙O的切線時，求證：∠PBD＝∠DAB；
（2）求證：BC2－CE2＝CE·DE.
查看答案和解析>>
科目：初中數學 來源： 題型：
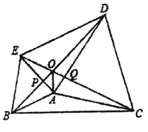
【題目】如圖，分別以
的邊
，
所在直線為對稱軸作的對稱圖形
和
，
，線段
與
相交于點
，連接
、
、
、
．有如下結論：①
；②
；③平分
；其中正確的結論個數是（ ）
A.0個B.3個C.2個D.1個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
