【題目】如圖，分別以
的邊
，
所在直線為對稱軸作的對稱圖形
和
，
，線段
與
相交于點
，連接
、
、
、
．有如下結論：①
；②
；③平分
；其中正確的結論個數是（ ）
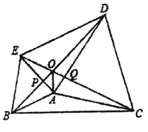
A.0個B.3個C.2個D.1個
【答案】B
【解析】
根據軸對稱的性質以及全等三角形的性質對每個結論進行一一判斷即可．
解：∵△ABD和△ACE是△ABC的軸對稱圖形，
∴∠BAD=∠CAE=∠BAC，AB=AE，AC=AD，
∴∠EAD=3∠BAC360°=3×150°360°=90°，故①正確；
∴∠ABE=∠CAD=
×(360°90°150°)=60°，
由翻折的性質得，∠AEC=∠ABD=∠ABC，
又∵∠EPO=∠BPA，
∴∠BOE=∠BAE=60°，故②正確；
在△ACE和△ADB中，
，
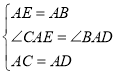∴△ACE≌△ADB，
∴S△ACE=S△ADB，BD=CE，
∴BD邊上的高與CE邊上的高相等，
即點A到∠BOC兩邊的距離相等，
∴OA平分∠BOC，故③正確；
綜上所述，結論正確的是①②③，
故選：B．
星級口算天天練系列答案
芒果教輔達標測試卷系列答案科目：初中數學 來源： 題型：
【題目】已知二次函數
的圖象如圖所示，有以下結論：
①abc＞0，
②a﹣b+c＜0，
③2a=b，
④4a+2b+c＞0，
⑤若點（﹣2，
）和（
，
）在該圖象上，則
．
其中正確的結論是 （填入正確結論的序號）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，E，F是正方形ABCD的邊CD上兩個動點，滿足DE＝CF．連接AE交BD于點I，連接BF交CI于點H，G為BC邊上的中點．若正方形的邊長為4，則線段DH長度的最小值是__________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某船自西向東航行，在
處測得某島
在北偏東
的方向上，前進
海里后到達
，此時，測得海島在北偏東
的方向上，要使船與海島最近，則船應繼續向東前進________海里．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（本題滿分8分）
如圖，點E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF與DE交于點O．
(1)求證：AB＝DC；
(2)試判斷△OEF的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校為了改善辦公條件，計劃從廠家購買
、
兩種型號電腦．已知每臺種型號電腦價格比每臺種型號電腦價格多0．1萬元，且用10萬元購買種型號電腦的數量與用8萬元購買種型號電腦的數量相同．求、兩種型號電腦每臺價格各為多少萬元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列條件中，不能判斷△ABC是直角三角形的是（ ）
A. a：b：c＝3：4：5 B. ∠A：∠B：∠C＝3：4：5
C. ∠A+∠B＝∠C D. a：b：c＝1：2：
查看答案和解析>>
科目：初中數學 來源： 題型：
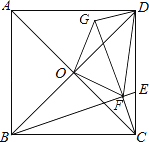
【題目】如圖，正方形ABCD的邊長為12，點O為對角線AC、BD的交點，點E在CD上，tan∠CBE= 
，過點C作CF⊥BE，垂足為F，連接OF，將△OCF繞著點O逆時針旋轉90°得到△ODG，連接FG、FD，則△DFG的面積是________．
查看答案和解析>>
科目：初中數學 來源： 題型：
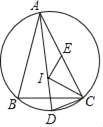
【題目】點I為△ABC的內心，連AI交△ABC的外接圓于點D，若AI=2CD，點E為弦AC的中點，連接EI，IC，若IC=6，ID=5，則IE的長為_____．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com