
 (x>0)的交點.
(x>0)的交點. (x>0)的圖象上另取一點B,作BK⊥x軸于K,在(2)的條件下,在線段OF上取一點C,使FO=4CO.試問:在y軸上是否存在點P,使得△PCA和△PBK的面積相等?若存在,求出所有可能的點P的坐標;若不存在,請說明理由.
(x>0)的圖象上另取一點B,作BK⊥x軸于K,在(2)的條件下,在線段OF上取一點C,使FO=4CO.試問:在y軸上是否存在點P,使得△PCA和△PBK的面積相等?若存在,求出所有可能的點P的坐標;若不存在,請說明理由. 的交點
的交點 ,
, ;
; ,2),
,2), k+b,
k+b, ,0)F(0,b)則:
,0)F(0,b)則: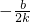 ,
, ),
), =2即b=4,
=2即b=4, ,
, +4;
+4;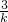 ),(0,4),
),(0,4), ×
× |y-1|;
|y-1|;
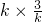 ;
; |y-1|
|y-1| =
= ×
×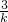 ×k,
×k,

科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
 19、某學校準備從甲、乙、丙、丁四位學生中選出一名學生做學生會干部,對四位學生進行了德、智、體、美、勞的綜合測試,四人成績如下表.同時又請100位同學對四位同學做推薦選舉投票,投票結果如扇形統計圖所示,學校決定綜合測試成績與民主推薦的分數比是6:4,即:綜合測試成績的60%和民主推薦成績的40%計入總成績.最后分數最高的當選為學生會干部.請你完成下列問題:
19、某學校準備從甲、乙、丙、丁四位學生中選出一名學生做學生會干部,對四位學生進行了德、智、體、美、勞的綜合測試,四人成績如下表.同時又請100位同學對四位同學做推薦選舉投票,投票結果如扇形統計圖所示,學校決定綜合測試成績與民主推薦的分數比是6:4,即:綜合測試成績的60%和民主推薦成績的40%計入總成績.最后分數最高的當選為學生會干部.請你完成下列問題:| 參加測試人員 | 甲 | 乙 | 丙 | 丁 |
| 綜合測試成績 | 74 | 73 | 66 | 75 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com