
【題目】如圖,在平面直角坐標系中,直線AC的表達式為![]() ,直線
,直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,有一動點
,有一動點![]() 在線段
在線段![]() 和線段
和線段![]() 上運動.
上運動.
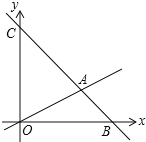
(1)求直線![]() 的表達式.
的表達式.
(2)求![]() 的面積.
的面積.
(3)是否存在點M,使![]() 的面積是
的面積是![]() 的面積的
的面積的![]() ?若存在請直接寫出點M的坐標.
?若存在請直接寫出點M的坐標.
【答案】(1)y=![]() x;(2)12;(3)M的坐標為(1,
x;(2)12;(3)M的坐標為(1,![]() )或(1,5).
)或(1,5).
【解析】
(1)利用待定系數法求直線OA的解析式;
(2)根據三角形面積公式計算;
(3)根據三角形的面積公式可判斷M的橫坐標是1,然后把x=1分別代入OA和AC的解析式中計算對應的函數值即可得到M點的坐標.
(1)設直線OA的表達式為y=kx,將點A(4,2)代入得2=4k,解得k=![]() ,
,
所以直線AB的解析式為y=![]() x;
x;
(2)在y=-x+6中,當x=0,y=6,則C(0,6),
S△OAC=![]() ×6×4=12;
×6×4=12;
(3)∵當△OMC的面積是△OAC的面積的![]() 時,
時,
∴M的橫坐標是![]() ×4=1,
×4=1,
當點M在線段OA上時,把x=1代入y=![]() x得y=
x得y=![]() ,則此時M(1,
,則此時M(1,![]() );
);
當點M在線段AC上時,把x=1代入y=-x+6得y=5,則此時M(1,5),
綜上所述,M的坐標為(1,![]() )或(1,5).
)或(1,5).


科目:初中數學 來源: 題型:
【題目】(觀察)
![]() ,
,![]() ,
,![]() ,……,
,……,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,……,
,……,![]() ,
,![]() ,
,![]() .
.
(發現)
根據你的閱讀回答問題:
(1)上述內容中,兩數相乘,積的最大值為______;
(2)設參與上述運算的第一個因數為![]() ,第二個因數為
,第二個因數為![]() ,用等式表示
,用等式表示![]() 與
與![]() 的數量關系是____.
的數量關系是____.
(類比)
觀察下列兩數的積:1×49,2×48,3×47,4×46,……m×n,……46×4,47×3,48×2,49×1
猜想![]() 的最大值為_______,并用你學過的知識加以證明.
的最大值為_______,并用你學過的知識加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(背景介紹)勾股定理是幾何學中的明珠,充滿著魅力.千百年來,人們對它的證明趨之若騖,其中有著名的數學家,也有業余數學愛好者.向常春在1994年構造發現了一個新的證法.

(小試牛刀)把兩個全等的直角三角形如圖1放置,其三邊長分別為a、b、c.顯然,∠DAB=∠B=90°,AC⊥DE.請用a、b、c分別表示出梯形ABCD、四邊形AECD、△EBC的面積,再探究這三個圖形面積之間的關系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四邊形AECD= ,
則它們滿足的關系式為 ,經化簡,可得到勾股定理.
(知識運用)(1)如圖2,鐵路上A、B兩點(看作直線上的兩點)相距40千米,C、D為兩個村莊(看作兩個點),AD⊥AB,BC⊥AB,垂足分別為A、B,AD=25千米,BC=16千米,則兩個村莊的距離為 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一個供應站P,使得PC=PD,請用尺規作圖在圖2中作出P點的位置并求出AP的距離.
(知識遷移)借助上面的思考過程與幾何模型,求代數式![]() 最小值(0<x<16)
最小值(0<x<16)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人進行射擊選拔賽,各射擊10發子彈,成績如下表:
環數命中 | 5環 | 6環 | 7環 | 8環 | 9環 | 10環 |
甲(次) | 1 | 1 | 1 | 3 | 2 | 2 |
乙(次) | 0 | 2 | 0 | 5 | 2 | 1 |
(1)計算甲、乙的平均成績.
(2)如果你是甲、乙的教練,你會選擇誰去參加正式比賽?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,E是BC的中點,連接AE并延長交DC的延長線于點F.

(1)求證:AB=CF;
(2)連接DE,若AD=2AB,求證:DE⊥AF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知△ABC中,AB=BC=1,∠ABC=90°,把一塊含30°角的直角三角板DEF的直角頂點D放在AC的中點上(直角三角板的短直角邊為DE,長直角邊為DF),將直角三角板DEF繞D點按逆時針方向旋轉.

(1)在圖1中,DE交邊AB于M,DF交邊BC于N,證明:DM=DN;
(2)在這一旋轉過程中,直角三角板DEF與△ABC的重疊部分為四邊形DMBN,請說明四邊形DMBN的面積是否發生變化?若發生變化,請說明是如何變化的?若不發生變化,求出其面積;
(3)繼續旋轉至如圖2的位置,延長AB交DE于M,延長BC交DF于N,DM=DN是否仍然成立?若成立,請給出證明;若不成立,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,兩直線l1:y=kx﹣2b+1和l2:y=(1﹣k)x+b﹣1交于x軸上一點A,與y軸分別交于點B、C,若A的橫坐標為2.
(1)求這兩條直線的解析式;
(2)求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明家的洗手盆上裝有一種抬啟式水龍頭(如圖1),完全開啟后,把手AM的仰角α=37°,此時把手端點A、出水口B和點落水點C在同一直線上,洗手盆及水龍頭的相關數據如圖2.(參考數據:sin37°=![]() ,cos37°=
,cos37°=![]() ,tan37°=
,tan37°=![]() )
)
求把手端點A到BD的距離;
求CH的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com