
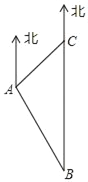
【題目】南沙群島是我國固有領(lǐng)土,現(xiàn)在我南海漁民要在南沙某海島附近進(jìn)行捕魚作業(yè),當(dāng)漁船航行至B處時,測得該島位于正北方向10(1+![]() )海里的C處,為了防止某國海巡警干擾,請求我A處的漁監(jiān)船前往C處護(hù)航.如圖,已知C位于A處的東北方向上,A位于B的北偏西30°方向上,則A和C之間的距離為( )
)海里的C處,為了防止某國海巡警干擾,請求我A處的漁監(jiān)船前往C處護(hù)航.如圖,已知C位于A處的東北方向上,A位于B的北偏西30°方向上,則A和C之間的距離為( )
A. 10![]() 海里 B. 20
海里 B. 20![]() 海里 C. 20
海里 C. 20![]() 海里 D. 10
海里 D. 10![]() 海里
海里
 應(yīng)用題作業(yè)本系列答案
應(yīng)用題作業(yè)本系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】2013年1月1日新交通法規(guī)開始實施.為了解某社區(qū)居民遵守交通法規(guī)情況,小明隨機(jī)選取部分居民就“行人闖紅燈現(xiàn)象”進(jìn)行問卷調(diào)查,調(diào)查分為“A:從不闖紅燈;B:偶爾闖紅燈;C:經(jīng)常闖紅燈;D:其他”四種情況,并根據(jù)調(diào)查結(jié)果繪制出部分條形統(tǒng)計圖(如圖1)和部分扇形統(tǒng)計圖(如圖2).請根據(jù)圖中信息,解答下列問題:
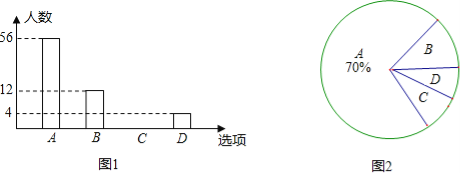
(1)本次調(diào)查共選取 名居民;
(2)求出扇形統(tǒng)計圖中“C”所對扇形的圓心角的度數(shù),并將條形統(tǒng)計圖補(bǔ)充完整;
(3)如果該社區(qū)共有居民1600人,估計有多少人從不闖紅燈?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小李在學(xué)校“青少年科技創(chuàng)新比賽”活動中,設(shè)計了一個沿直線軌道做勻速直線運動的模型.甲車從![]() 處出發(fā)向
處出發(fā)向![]() 處行駛,同時乙車從
處行駛,同時乙車從![]() 處出發(fā)向
處出發(fā)向![]() 處行駛.如圖所示,線段
處行駛.如圖所示,線段![]() 、
、![]() 分別表示甲車、乙車離
分別表示甲車、乙車離![]() 處的距離
處的距離![]() (米)與已用時間
(米)與已用時間![]() (分)之間的關(guān)系.試根據(jù)圖象,解決以下問題:
(分)之間的關(guān)系.試根據(jù)圖象,解決以下問題:
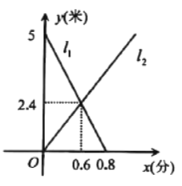
(1)填空:出發(fā)_________(分)后,甲車與乙車相遇,此時兩車距離![]() 處________(米);
處________(米);
(2)求乙車行駛![]() (分)時與
(分)時與![]() 處的距離.
處的距離.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
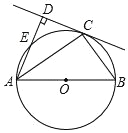
【題目】如圖,AB 為⊙O 的直徑,點 C 為⊙O 上一點,AD 和過點 C 的切線相互垂直,垂足為 D.
(1)求證:AC 平分∠DAB;
(2)AD 交⊙O 于點 E,若 AD=3CD=9,求 AE 的長度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
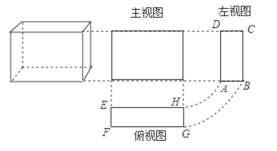
【題目】張師傅根據(jù)某幾何體零件,按1:1的比例畫出準(zhǔn)確的三視圖(都是長方形)如圖,已知EF=4cm,F(xiàn)G=12cm,AD=10cm.
(1)說出這個幾何體的名稱;
(2)求這個幾何體的表面積S;
(3)求這個幾何體的體積V.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
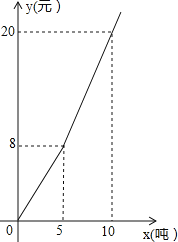
【題目】浙江實施“五水共治“以來,越來越重視節(jié)約用水,某地對居民用水按階梯水價方式進(jìn)行收費,人均月生活用水收費標(biāo)準(zhǔn)如圖所示,圖中x表示人均月生活用水的噸數(shù),y表示收取的人均月生活用水費(元),請根據(jù)圖象信息,回答下列問題.
(1)請寫出y與x的函數(shù)關(guān)系式;
(2)若某個家庭有5人,響應(yīng)節(jié)水號召,計劃控制1月份的生活用水費不超過76元,則該家庭這個月最多可以用多少噸水?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩家藍(lán)莓采摘園的藍(lán)莓品質(zhì)相同,銷售價格都是每千克30元,兩家均推出了“周末”優(yōu)惠方案.甲采摘園的優(yōu)惠方案是:游客進(jìn)園需購買60元的門票,采摘的藍(lán)莓六折優(yōu)惠;乙采摘園的優(yōu)惠方案是:游客進(jìn)園不需要購買門票,采摘的藍(lán)莓超過10千克后,超過部分五折優(yōu)惠.優(yōu)惠期間,設(shè)某游客的藍(lán)莓采摘量為![]() 千克,在甲采摘園所需總費用為
千克,在甲采摘園所需總費用為![]() 元,在乙采摘園所需總費用為
元,在乙采摘園所需總費用為![]() 元.
元.
(1)求![]() ,
,![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)該游客如何選擇采摘園去采摘比較合算?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如果m是從0,1,2,3四個數(shù)中任取的一個數(shù),n是從0,1,2三個數(shù)中任取的一個數(shù),那么關(guān)于x的一元二次方程x2-2mx+n2=0有實數(shù)根的概率為______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
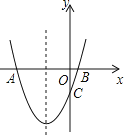
【題目】如圖,拋物線y=x2+2x+k+1與x軸交與A、B兩點,與y軸交與點C(0,-3).
(1)求拋物線的對稱軸及k的值;
(2)求拋物線的對稱軸上存在一點P,使得PA+PC的值最小,求此時點P的坐標(biāo);
(3)點M是拋物線上的一動點,且在第三象限.
①當(dāng)M點運動到何處時,△AMB的面積最大?求出△AMB的最大面積及此時點M的坐標(biāo).
②當(dāng)M點運動到何處時,四邊形AMCB的面積最大?求出四邊形AMCB的最大面積及此時點M的坐標(biāo).
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com