
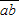 =4(a+b),即10a+b=4(a+b),亦即2a=b,因此兩位數的四合數為12,24,36,48,它們的總和為12+24+36+48=120.
=4(a+b),即10a+b=4(a+b),亦即2a=b,因此兩位數的四合數為12,24,36,48,它們的總和為12+24+36+48=120.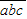 =4(a+b+c),即100a+10b+c=4(a+b+c),亦即96a+6b=3c.因為a≥1,b≥0,c≤9,所以此方程無解.因此三位數的四合數不存在.同樣的分析可知三位數以上的四合數也不存在.
=4(a+b+c),即100a+10b+c=4(a+b+c),亦即96a+6b=3c.因為a≥1,b≥0,c≤9,所以此方程無解.因此三位數的四合數不存在.同樣的分析可知三位數以上的四合數也不存在.

 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案科目:初中數學 來源: 題型:閱讀理解
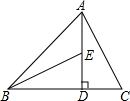
| 5 |
| 5 |
| 3 |
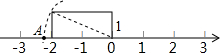
查看答案和解析>>
科目:初中數學 來源:專項題 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com