Question

解不等式組，并將解集在數軸上表示出來．
（1）

3(x+2)＜x+4 x 3 ≥ x+1 4

（2）

2x-3＜9-x 10-3x＜2x-5

（3）解不等式

1-x

4

＞1-

1-2x

2

，并寫出它的最大整數解．

Answer 1

分析：（1）、（2）先求組成不等式組的兩個不等式的解集，然后再求兩個不等式的交集，該交集就是不等式的解集；
（3）先去分母，再移項、合并同類項，最后求解集．

解答：解：（1）由不等式3（x+2）＜x+4，得
2x＜-2，即x＞-1；
由不等式

x

3

≥

x+1

4

，得
4x≥3x+3，即x≥3；
所以，原不等式組的解集是x≥3；


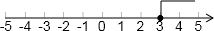
（2）由不等式2x-3＜9-x，得
3x＜12，即x＜4；
由不等式10-3x＜2x-5，得
-5x＜-15，即x＞3，
所以，原不等式組的解集是3＜x＜4；


（3）由原不等式的兩邊同時乘以4，得
1-x＞2+4x，
移項、合并同類項，得
-5x＞1，
不等式的兩邊同時除以-5（不等號的方向發生改變），得
x＜-

1

5

；

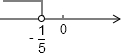
由不等式的解集在數軸上的顯示，知
原不等式的最大整數解是-1．

點評：不等式的解集在數軸上表示出來的方法：“＞”空心圓點向右畫折線，“≥”實心圓點向右畫折線，“＜”空心圓點向左畫折線，“≤”實心圓點向左畫折線．