Question

（1）解方程：

x-1

2

-

2x+3

3

=1
（2）解方程組：

x+y=9 3(x+y)+2x=33

（3）解不等式組，并將解集在數軸上表示出來：

3(x+1)＜2x+3 x-1 3 ≤ x 2

．

Answer 1

分析：（1）這是一個帶分母的方程，所以要先去分母，再去括號，最后移項，合并同類項，系數化為1，從而得到方程的解；
（2）把（x+y）看作一個整體，代入第二個方程，利用代入消元法求解即可；
（3）先求出兩個不等式的解集，再求其公共解．

解答：解：（1）去分母得，3（x-1）-2（2x+3）=6，
去括號得，3x-3-4x-6=6，
移項得，3x-4x=6+3+6，
合并同類項得，-x=15，
系數化為1得，x=-15；

（2）

x+y=9① 3(x+y)+2x=33②

，
①代入②得，3×9+2x=33，
解得x=3，
把x=3代入①得，3+y=9，
解得y=6，
所以，方程組的解是

x=3 y=6

；

（3）

3(x+1)＜2x+3① x-1 3 ≤ x 2 ②

，
解不等式①，得x＜0，
解不等式②，得x≥-2，
在數軸上表示如下：

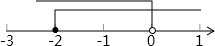
所以，此不等式組的解集是-2≤x＜0．

點評：（1）考查了解一元一次方程，注意在去分母時，方程兩端同乘各分母的最小公倍數時，不要漏乘沒有分母的項，同時要把分子（如果是一個多項式）作為一個整體加上括號；
（2）考查的是二元一次方程組的解法，利用整體思想代入求解更加簡便；
（3）考查了一元一次不等式組的解法，在數軸上表示不等式組的解集，需要把每個不等式的解集在數軸上表示出來（＞，≥向右畫；＜，≤向左畫），在表示解集時“≥”，“≤”要用實心圓點表示；“＜”，“＞”要用空心圓點表示．