
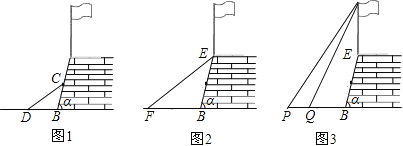
【題目】九(1)班同學在上學期的社會實踐活動中,對學校旁邊的山坡護墻和旗桿進行了測量.
(1)如圖1,第一小組用一根木條CD斜靠在護墻上,使得DB與CB的長度相等,如果測量得到∠CDB=38°,求護墻與地面的傾斜角α的度數.
(2)如圖2,第二小組用皮尺量的EF為16米(E為護墻上的端點),EF的中點離地面FB的高度為1.9米,請你求出E點離地面FB的高度.
(3)如圖3,第三小組利用第一、第二小組的結果,來測量護墻上旗桿的高度,在點P測得旗桿頂端A的仰角為45°,向前走4米到達Q點,測得A的仰角為60°,求旗桿AE的高度(精確到0.1米).
備用數據:![]() .
.
【答案】(1)76°;(2)3.8米;(3)5.7米.
【解析】
試題(1)根據∠α=2∠CDB即可得出答案.
(2)設EF的中點為M,過M作MN⊥BF,垂足為點N,過點E作EH⊥BF,垂足為點H,根據EH=2MN即可求出E點離地面FB的高度;
(3)延長AE,交PB于點C,設AE=x,則AC=x+3.8,CQ=x﹣0.2,根據![]() ,得出
,得出![]() ,求出x即可.
,求出x即可.
試題解析:解:(1)∵BD=BC,∴∠CDB=∠DCB.
∴∠α=2∠CDB=2×38°=76°.
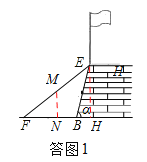
(2)如答圖1,設EF的中點為M,過M作MN⊥BF,垂足為點N,過點E作EH⊥BF,垂足為點H,
∵MN∥AH,MN=1.9,∴EH=2MN=3.8(米).
∴E點離地面FB的高度是3.8米.
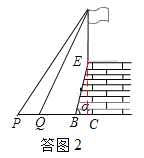
(3)如答圖2,延長AE,交PB于點C,
設AE=x,則AC=x+3.8,
∵∠APB=45°,∴PC=AC=x+3.8.
∵PQ=4,∴CQ=x+3.8﹣4=x﹣0.2.
∵![]() ,
,
∴![]() ,解得
,解得![]() .
.
∴AE≈5.7(米).
答;旗桿AE的高度是5.7米.


科目:初中數學 來源: 題型:
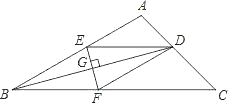
【題目】如圖,在 ABC 中,BD 平分ABC 交 AC 于 D ,EF 垂直平分 BD ,分別交 AB, BC, BD于 E, F , G ,連接 DE, DF 。
(1)求證:四邊形 BEDF 為菱形;
(2)若ABC 30, C 45, DE 4 ,求CF 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,D是BC邊上一點,以DB為直徑的⊙O經過AB的中點E,交AD的延長線于點F,連接EF.
(1)求證:∠1=∠F;
(2)若sinB=![]() ,EF=2
,EF=2![]() ,求CD的長.
,求CD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
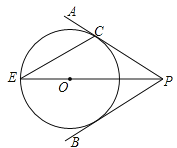
【題目】如圖,點O在∠APB的平分線上,⊙O與PA相切于點C.
(1)求證:直線PB與⊙O相切;
(2)PO的延長線與⊙O交于點E.若⊙O的半徑為3,PC=4.求弦CE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC在網格中的位置如圖所示(每個小正方形邊長為1),AD⊥BC于D,下列選項中,錯誤的是( )

A. sinα=cosα B. tanC=2 C. sinβ=![]() D. tanα=1
D. tanα=1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC的頂點A,C分別在x軸和y軸上,點B的坐標為(2,3),雙曲線y=![]() (x>0)的圖象經過BC上的點D與AB交于點E,連接DE,若E是AB的中點.
(x>0)的圖象經過BC上的點D與AB交于點E,連接DE,若E是AB的中點.
(1)求點D的坐標;
(2)點F是OC邊上一點,若△FBC和△DEB相似,求點F的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
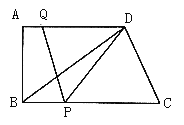
【題目】如圖所示,在四邊形ABCD中,AD//BC,∠A=90°,AB=12,BC=21,AD=16.動點P從點B出發,沿射線BC的方向以每秒2個單位長的速度運動,動點Q同時從點A出發,在線段AD上以每秒1個單位長的速度向點D運動,當其中一個動點到達端點時另一個動點也隨之停止運動.設運動的時間為t(秒).
(1)設△DPQ的面積為S,求S與t之間的函數關系式;
(2)分別求出出當t為何值時,①PD=PQ,②DQ=PQ?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了培養學生的社會實踐能力,今年“五一”長假期間要求學生參加一項社會調查活動.為此,小明在他所居住小區的600個家庭中,隨機調查了50個家庭在新工資制度實施后的收入情況,并繪制了如下的頻數分布表和頻數分布直方圖(收入取整數,單位:元).
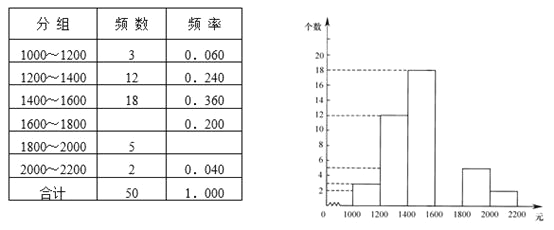
請你根據以上提供的信息,解答下列問題:
(1)補全頻數分布表和頻數分布直方圖;
(2)這50個家庭收入的中位數落在 小組;
(3)請你估算該小區600個家庭中收入較低(不足1400元)的家庭個數大約有多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com