
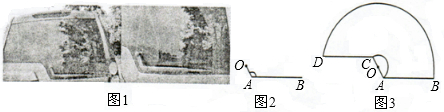
如圖1,一輛汽車的背面,有一種特殊形狀的刮雨器,忽略刮雨器的寬度可抽象為一條折線OAB,如圖2所示,量得連桿OA長為10cm,雨刮桿AB長為48cm,∠OAB=1200.若啟動一次刮雨器,雨刮桿AB正好掃到水平線CD的位置,如圖3所示.
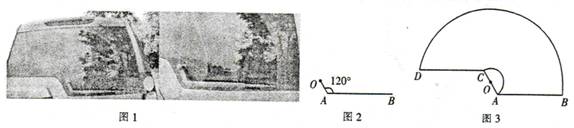
(1)求雨刮桿AB旋轉的最大角度及O、B兩點之間的距離;(結果精確到0.01)
(2)求雨刮桿AB掃過的最大面積.(結果保留π的整數(shù)倍)
(參考數(shù)據(jù):sin60°= ,cos60°=
,cos60°=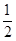 ,tan60°=
,tan60°=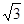 ,
,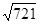 ≈26.851,可使用科學計算器)
≈26.851,可使用科學計算器)
解:(1)∵從點A 旋轉到點C為1800,
∴雨刮桿AB旋轉的最大角度為1800。
連接OB,過O點作AB的垂線交BA的延長線于EH,
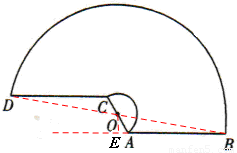
∵∠OAB=1200°,∴∠OAE=60°。
在Rt△OAE中,∵∠OAE=600°,OA=10,
∴ ,
,
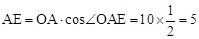 。
。
∵AB=48,∴EB=AE+AB=53。
在Rt△OEB中,∵OE=
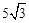 ,EB=53,
,EB=53,
∴ (cm)。
(cm)。
∴O、B兩點之間的距離為53.70 cm。
(2)∵雨刮桿AB旋轉180°得到CD,即△OCD與△OAB關于點O中心對稱,
∴△BAO≌△OCD。∴S△BAO=S△OCD。
∴雨刮桿AB掃過的最大面積S=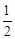 π(OB2-OA2) =1392π(cm2)。
π(OB2-OA2) =1392π(cm2)。
【解析】
試題分析:(1)AB旋轉的最大角度為180°;在△OAB中,已知兩邊及其夾角,可求出另外兩角和一邊,只不過它不是直角三角形,需要轉化為直角三角形來求解,由∠OAB=1200想到作AB邊上的高,得到一個含600角的Rt△OAE和一個非特殊角的Rt△OEB。在Rt△OAE中,已知∠OAE=600,斜邊OA=10,可求出OE、AE的長,從而求得Rt△OEB中EB的長,再由勾股定理求出斜邊OB的長。
(2)根據(jù)旋轉的性質可知,雨刮桿AB掃過的最大面積就是一個半圓環(huán)的面積(以OB、OA為半徑的半圓面積之差)。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數(shù)學 來源: 題型:
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 721 |
查看答案和解析>>
科目:初中數(shù)學 來源:2013年初中畢業(yè)升學考試(江西卷)數(shù)學(解析版) 題型:解答題
如圖1,一輛汽車的背面,有一種特殊形狀的刮雨器,忽略刮雨器的寬度可抽象為一條折線OAB,如圖2所示,量得連桿OA長為10cm,雨刮桿AB長為48cm,∠OAB=1200.若啟動一次刮雨器,雨刮桿AB正好掃到水平線CD的位置,如圖3所示.
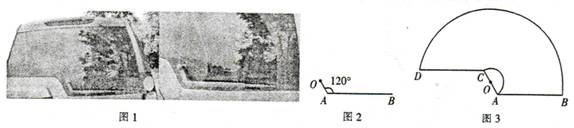
(1)求雨刮桿AB旋轉的最大角度及O、B兩點之間的距離;(結果精確到0.01)
(2)求雨刮桿AB掃過的最大面積.(結果保留π的整數(shù)倍)
(參考數(shù)據(jù):sin60°=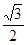 ,cos60°=
,cos60°=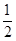 ,tan60°=
,tan60°=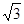 ,
,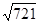 ≈26.851,可使用科學計算器)
≈26.851,可使用科學計算器)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 ,cos60°=
,cos60°= ,tan60°=
,tan60°= ,
,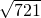 ≈26.851,可使用科學記算器)
≈26.851,可使用科學記算器)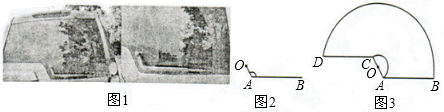
查看答案和解析>>
科目:初中數(shù)學 來源:2013年江西省南昌市中考數(shù)學試卷(解析版) 題型:解答題
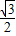 ,cos60°=
,cos60°= ,tan60°=
,tan60°=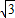 ,
,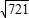 ≈26.851,可使用科學記算器)
≈26.851,可使用科學記算器)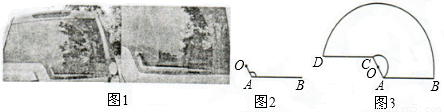
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com