
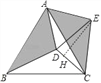
【題目】如圖,在等邊△ABC內有一點D,AD=5,BD=6,CD=4,將△ABD繞A點逆時針旋轉,使AB與AC重合,點D旋轉至點E.
(1)DE=_____;
(2)∠CDE的正切值為_____.

【答案】 5, 3![]()
【解析】分析:(1)先利用等邊三角形的性質AB=AC,∠BAC=60°,再根據旋轉的性質得AD=AE, ∠DAE=∠BAC=60°,CE=BD=6,然后判斷△ADE為等邊三角形得到DE的長;(2) 作EH⊥CD于H, 設DH=x,則CH=4﹣x,利用勾股定理得到52﹣x2=62﹣(4-x),解得x=![]() ,再計算出EH的長,然后利用正切的定義求解.
,再計算出EH的長,然后利用正切的定義求解.
詳解:(1)∵△ABC為等邊三角形,
∴AB=AC,∠BAC=60°,
∵△ABD繞A點逆時針旋轉,使AB與AC重合,點D旋轉至點E,
∴AD=AE,∠DAE=∠BAC=60°,CE=BD=6,
∴△ADE為等邊三角形,
∴DE=AD=5;
(2)作EH⊥CD于H,如圖,
設DH=x,則CH=4﹣x,
在Rt△EDH中,EH2=DE2﹣DH2=52﹣x2,
在Rt△ECH中,EH2=CE2﹣CH2=62﹣(4﹣x)2,
∴52﹣x2=62﹣(4﹣x)2,解得x=![]() ,
,
∴EH=![]() =
=![]() ,
,
∴tan∠EDH=![]() =3
=3![]() ,
,
即∠CDE的正切值為3![]() .
.
故答案為5,3![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,港口A在觀測站O的正東方向,OA=40海里,某船從港口A出發,沿北偏東15°方向航行半小時后到達B處,此時從觀測站O處測得該船位于北偏東60°的方向.求該船航行的速度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=2,BC=4,P為矩形邊上的一個動點,運動路線是A→B→C→D→A,設P點經過的路程為x,以A,P,B為頂點的三角形面積為y,則選項圖象能大致反映y與x的函數關系的是( )
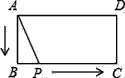
A. 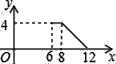 B.
B. 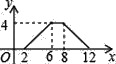 C.
C. 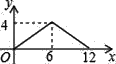 D.
D. 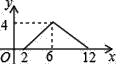
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正方形ABCD,P為射線AB上的一點,以BP為邊作正方形BPEF,使點F在線段CB的延長線上,連接EA,EC.

(1)如圖1,若點P在線段AB的延長線上,求證:EA=EC;
(2)如圖2,若點P在線段AB的中點,連接AC,判斷△ACE的形狀,并說明理由;
(3)如圖3,若點P在線段AB上,連接AC,當EP平分∠AEC時,設AB=a,BP=b,求a:b及∠AEC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,AB為⊙O的直徑,AD平分∠CAB,AC⊥CD,垂足為C.
(1)判斷CD與⊙O的位置關系,并說明理由;
(2)求證:∠CDA=∠AED.

查看答案和解析>>
科目:初中數學 來源: 題型:
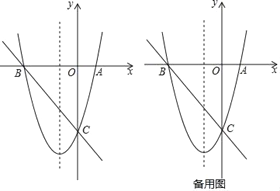
【題目】如圖,已知拋物線y=![]() x2+3x﹣8的圖象與x軸交于A,B兩點(點A在點B的右側),與y軸交于點C.
x2+3x﹣8的圖象與x軸交于A,B兩點(點A在點B的右側),與y軸交于點C.
(1)求直線BC的解析式;
(2)點F是直線BC下方拋物線上的一點,當△BCF的面積最大時,在拋物線的對稱軸上找一點P,使得△BFP的周長最小,請求出點F的坐標和點P的坐標;
(3)在(2)的條件下,是否存在這樣的點Q(0,m),使得△BFQ為等腰三角形?如果有,請直接寫出點Q的坐標;如果沒有,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
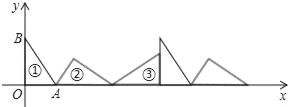
【題目】如圖①為Rt△AOB,∠AOB=90°,其中OA=3,OB=4.將AOB沿x軸依次以A,B,O為旋轉中心順時針旋轉.分別得圖②,圖③,…,則旋轉到圖⑩時直角頂點的坐標是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列因式分解的過程,再回答所提出的問題:
1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]
=(1+x)2(1+x)
=(1+x)3
(1)上述分解因式的方法是 ,共應用了 次.
(2)若分解1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004,則需應用上述方法 次,結果是 .
(3)分解因式:1+x+x(x+1)+x(x+1)2+…+ x(x+1)n(n為正整數).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com