
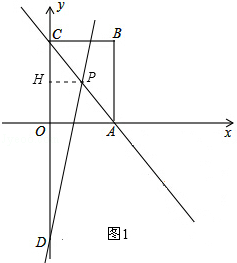
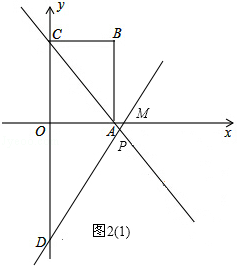
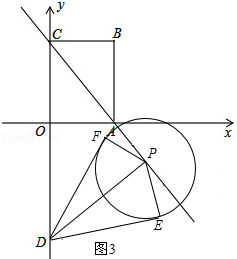
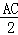 ,過點(diǎn)D作動圓P的兩條切線與動圓P分別相切于點(diǎn)E、F.請?zhí)角笤趧訄AP中是否存在面積最小的四邊形DEPF?若存在,請求出最小面積S的值;若不存在,請說明理由.
,過點(diǎn)D作動圓P的兩條切線與動圓P分別相切于點(diǎn)E、F.請?zhí)角笤趧訄AP中是否存在面積最小的四邊形DEPF?若存在,請求出最小面積S的值;若不存在,請說明理由.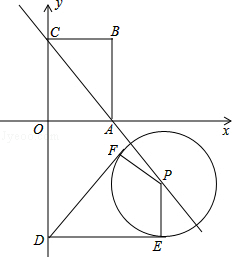
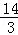 x﹣5
x﹣5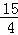 ,0)或(
,0)或(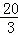 ,0)
,0)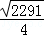
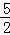 DE.由∠DEP=90°得DE2=DP2﹣PE2=DP2﹣
DE.由∠DEP=90°得DE2=DP2﹣PE2=DP2﹣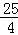 .根據(jù)“點(diǎn)到直線之間,垂線段最短”可得:當(dāng)DP⊥AC時(shí),DP最短,此時(shí)DE也最短,對應(yīng)的四邊形DEPF的面積最小.借助于三角形相似,即可求出DP⊥AC時(shí)DP的值,就可求出四邊形DEPF面積的最小值.
.根據(jù)“點(diǎn)到直線之間,垂線段最短”可得:當(dāng)DP⊥AC時(shí),DP最短,此時(shí)DE也最短,對應(yīng)的四邊形DEPF的面積最小.借助于三角形相似,即可求出DP⊥AC時(shí)DP的值,就可求出四邊形DEPF面積的最小值.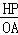 =
=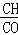 =
=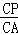 .
. CA.
CA. OA,CH=
OA,CH= CO.
CO.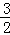 ,CH=2.
,CH=2.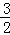 ,2).
,2).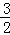 ,2)在直線DP上,
,2)在直線DP上,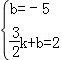
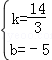
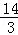 x﹣5.
x﹣5.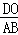 =
=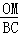 .
.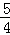 =
=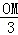 .
.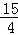 .
.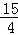 ,0)
,0)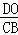 =
=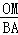 .
.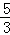 =
=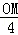 .
.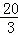 .
.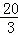 ,0).
,0).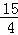 ,0)或(
,0)或(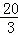 ,0).
,0).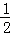 AC=
AC=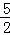 .
.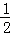 PE•DE=PE•DE=
PE•DE=PE•DE=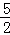 DE.
DE.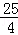 .
.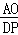 =
=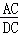 .
.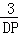 =
=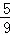 .
.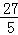 .
.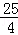 =(
=(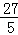 )2﹣
)2﹣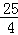 =
=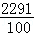 .
.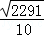 ,
,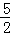 DE=
DE=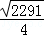 .
.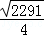 .
.


 一線名師權(quán)威作業(yè)本系列答案
一線名師權(quán)威作業(yè)本系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源:不詳 題型:填空題
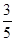 ,OA=10cm,則AB長為 cm.
,OA=10cm,則AB長為 cm.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:不詳 題型:單選題
| A.2r=R | B.
| C.3r=R | D.4r=R |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:不詳 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:不詳 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:不詳 題型:單選題
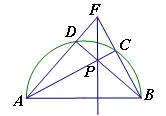
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com