
【題目】如圖,![]() 是邊長為9的等邊三角形,
是邊長為9的等邊三角形,![]() 是
是![]() 邊上一動點,由
邊上一動點,由![]() 向
向![]() 運動(與
運動(與![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延長線上一動點,與點
延長線上一動點,與點![]() 同時以相同的速度由
同時以相同的速度由![]() 向
向![]() 延長線方向運動(
延長線方向運動(![]() 不與
不與![]() 重合),過
重合),過![]() 作
作![]() 于
于![]() ,連接
,連接![]() 交
交![]() 于
于![]()

(1)若![]() 時,求
時,求![]() 的長
的長
(2)當點![]() ,
,![]() 運動時,線段
運動時,線段![]() 與線段
與線段![]() 是否相等?請說明理由
是否相等?請說明理由
(3)在運動過程中線段![]() 的長是否發生變化?如果不變,求出線段
的長是否發生變化?如果不變,求出線段![]() 的長;如果發生變化,請說明理由
的長;如果發生變化,請說明理由
【答案】(1)當∠BQD=30° 時,AP=3;(2)相等,見解析;(3)DE的長不變,![]()
【解析】
(1)先判斷出∠QPC是直角,再利用含30°的直角三角形的性質得出QC=2PC,建立方程求解決即可;
(2)先作出PF∥BC得出∠PFA=∠FPA=∠A=60°,進而判斷出△DBQ≌△DFP得出DQ=DP即可得出結論;
(3)利用等邊三角形的性質得出EF=![]() AF,借助DF=DB,即可得出DF=
AF,借助DF=DB,即可得出DF=![]() BF,最后用等量代換即可.
BF,最后用等量代換即可.
(1)解:∵△ABC是邊長為9的等邊三角形
∴∠ACB=60°,且∠BQD=30°
∴∠QPC=90°
設AP=![]() ,則PC=
,則PC=![]() ,QB=
,QB=![]()
∴QC=![]()
∵在Rt△QCP中,∠BQD=30°
∴PC=![]() QC 即
QC 即![]()
解得![]()
∴ 當∠BQD=30° 時,AP=3
(2)相等,
證明:過P作PF∥QC,則△AFP是等邊三角形
∴AP=PF,∠DQB=∠DPF
∵P、Q同時出發,速度相同,即BQ=AP,
∴BQ=PF,
在△DBQ和△DFP中,
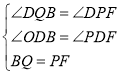
∴△DBQ≌△DFP(AAS)
∴QD=PD
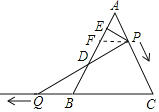
(3)解:不變,
由(2)知△DBQ≌△DFP
∴BD=DF
∵△AFP是等邊三角形,PE⊥AB,
∴AE=EF,
∴DE=DF+EF=![]() BF+
BF+![]() FA=
FA=![]() AB=
AB=![]() 為定值,即DE的長不變.
為定值,即DE的長不變.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:初中數學 來源: 題型:
【題目】如圖,∠C=90°,AD平分∠BAC,DE⊥AB于點E,有下列結論:①CD=ED ;②AC+ BE= AB ;③DA平分∠CDE ;④∠BDE =∠BAC;⑤![]() =AB:AC.其中結論正確的個數有()
=AB:AC.其中結論正確的個數有()
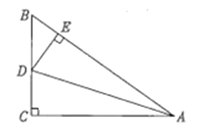
A.5個B.4個
C.3個D.2個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】針對下列圖象李明同學說到:圖①可能是![]() ;圖②可能是
;圖②可能是![]() ;圖③可能是
;圖③可能是![]() ;圖④可能是
;圖④可能是![]()
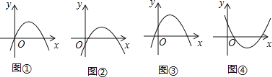
你認為其中必定正確的有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個大小不同的等腰直角三角形三角板如圖1所示放置,圖2是由它抽象出的幾何圖,點![]() ,
,![]() ,
,![]() 在同一條直線上,連結DC
在同一條直線上,連結DC

(1)請判斷![]() 與
與![]() 的位置關系,并證明
的位置關系,并證明
(2)若![]() ,
,![]() ,求
,求![]() 的面積
的面積
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中央電視臺的“朗讀者”節目激發了同學們的讀書熱情,為了引導學生“多讀書,讀好書“,某校對八年級部分學生的課外閱讀量進行了隨機調查,整理調查結果發現,學生課外閱讀的本書最少的有5本,最多的有8本,并根據調查結果繪制了不完整的圖表,如圖所示:
本數(本) | 頻數(人數) | 頻率 |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
合計 | 50 | c |
我們定義頻率=![]() ,比如由表中我們可以知道在這次隨機調查中抽樣人數為50人課外閱讀量為6本的同學為18人,因此這個人數對應的頻率就是
,比如由表中我們可以知道在這次隨機調查中抽樣人數為50人課外閱讀量為6本的同學為18人,因此這個人數對應的頻率就是![]() =0.36.
=0.36.
(1)統計表中的a、b、c的值;
(2)請將頻數分布表直方圖補充完整;
(3)求所有被調查學生課外閱讀的平均本數;
(4)若該校八年級共有600名學生,你認為根據以上調查結果可以估算分析該校八年級學生課外閱讀量為7本和8本的總人數為多少嗎?請寫出你的計算過程.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,函數 y kx 與 y  的圖象交于 A、B 兩點,過 A 作 y 軸的垂線,交函數
的圖象交于 A、B 兩點,過 A 作 y 軸的垂線,交函數 的圖象于點 C,連接 BC,則△ABC 的面積為( )
的圖象于點 C,連接 BC,則△ABC 的面積為( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將如圖所示的牌面數字分別是1,2,3,4的四張撲克牌背面朝上,洗勻后放在桌面上.
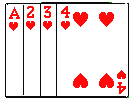
(1)從中隨機抽出一張牌,牌面數字是偶數的概率是 ;
(2)從中隨機抽出二張牌,兩張牌牌面數字的和是5的概率是 ;
(3)先從中隨機抽出一張牌,將牌面數字作為十位上的數字,然后將該牌放回并重新洗勻,再隨機抽取一張,將牌面數字作為個位上的數字,請用畫樹狀圖或列表的方法求組成的兩位數恰好是4的倍數的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(12分)如圖①,∠QPN的頂點P在正方形ABCD兩條對角線的交點處,∠QPN=α,將∠QPN繞點P旋轉,旋轉過程中∠QPN的兩邊分別與正方形ABCD的邊AD和CD交于點E和點F(點F與點C,D不重合).
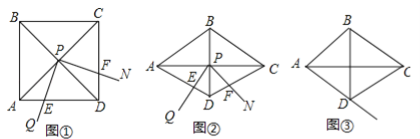
(1)如圖①,當α=90°時,DE,DF,AD之間滿足的數量關系是 ;
(2)如圖②,將圖①中的正方形ABCD改為∠ADC=120°的菱形,其他條件不變,當α=60°時,(1)中的結論變為DE+DF=![]() AD,請給出證明;
AD,請給出證明;
(3)在(2)的條件下,若旋轉過程中∠QPN的邊PQ與射線AD交于點E,其他條件不變,探究在整個運動變化過程中,DE,DF,AD之間滿足的數量關系,直接寫出結論,不用加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D是直角等腰△ABC斜邊AB的中點,M為邊AC上不和A、C重合的一動點,聯結DM,過D作DNDM,交BC于N,聯結MN.
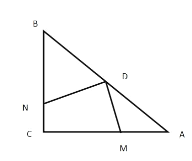
(1)求證:以AM、MN、BN為邊的三角形是直角三角形
(2)如果AC2,AMx,試用x表示△DMN的面積,并求當ADM22.5時△DMN的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com