【題目】如圖，點D是直角等腰△ABC斜邊AB的中點，M為邊AC上不和A、C重合的一動點，聯結DM，過D作DNDM，交BC于N，聯結MN．
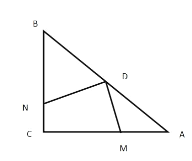
(1)求證：以AM、MN、BN為邊的三角形是直角三角形
(2)如果AC2，AMx，試用x表示△DMN的面積，并求當ADM22．5時△DMN的面積．
【答案】（1）見解析；（2）
，
【解析】
（1）連接
、MN，結合等腰直角三角形的性質利用ASA可證
，由全等三角形的性質可得
，
，由
是直角三角形可知以
為邊的三角形時直角三角形；
（2）易知
，
，由勾股定理可得MN長，由（1）中可知
，結合勾股定理可知MD長，根據三角形面積公式可用x表示出△DMN的面積，當ADM22．5時，可得
，在
中，根據勾股定理可得CD長，求出x值代入△DMN的面積的表達式中即可求解.
（1） 如圖，連接、MN，
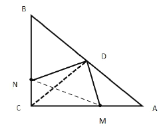
是等腰直角三角形
點D是AB的中點
在
和
中，
∴
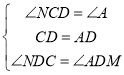
是直角三角形，即以
為邊的三角形時直角三角形
∴以為邊的三角形時直角三角形
（2），由（1）知
在
中，根據勾股定理得
，
在
中，根據勾股定理得
即 
，
所以
當
時，
，
，
在
中，根據勾股定理得
由（1）知
，
，解得
將代入得
.
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】如圖，
是邊長為9的等邊三角形，
是
邊上一動點，由
向
運動（與、不重合），
是
延長線上一動點，與點同時以相同的速度由
向延長線方向運動（不與重合），過作
于
，連接
交
于
（1）若
時，求
的長
（2）當點，運動時，線段
與線段
是否相等？請說明理由
（3）在運動過程中線段
的長是否發生變化？如果不變，求出線段的長；如果發生變化，請說明理由
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖, 在東西方向的海岸線MN上有A，B兩港口，海上有一座小島P，漁民每天都乘輪船從A，B 兩港口沿AP，BP的路線去小島捕魚作業．已知小島P在A港的北偏東60°方向，在B港的北偏西45°方向，小島P距海岸線MN的距離為30海里.
(1)求AP，BP的長(參考數據：
≈1.4，
≈1.7，
≈2.2)；
(2)甲、乙兩船分別從A，B兩港口同時出發去小島P捕魚作業，甲船比乙船晚到小島24分鐘．已知甲船速度是乙船速度的1.2倍，利用(1)中的結果求甲、乙兩船的速度各是多少海里/時？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校八年級數學課外興趣小組的同學積極參加義工活動，小慶對全體小組成員參加活動次數的情況進行統計解析，繪制了如下不完整的統計表和統計圖（圖）．
次數 | 10 | 8 | 6 | 5 |
人數 | 3 | a | 2 | 1 |
（1）表中a= ；
（2）請將條形統計圖補充完整；
（3）從小組成員中任選一人向學校匯報義工活動情況，參加了10次活動的成員被選中的概率有多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①，在平面直角坐標系中，圓心為P（x，y）的動圓經過點A（2，8），且與x軸相切于點B.
(1)當x＞0，y=5時，求x的值；
(2)當x = 6時，求⊙P的半徑；
(3)求y關于x的函數表達式，請判斷此函數圖象的形狀，并在圖②中畫出此函數的圖象（不必列表，畫草圖即可）.
圖① 圖②
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，海中有一小島P，在距小島P的
海里范圍內有暗礁，一輪船自西向東航行，它在A處時測得小島P位于北偏東60°，且A、P之間的距離為32海里，若輪船繼續向正東方向航行，輪船有無觸礁危險？請通過計算加以說明．如果有危險，輪船自A處開始至少沿東偏南多少度方向航行，才能安全通過這一海域？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，△ABC的三個頂點分別為A（－1，4），B（－5，3），C（－3，2）．
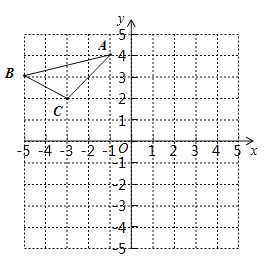
（1）將△ABC向下平移6個單位后得到△A1B1C1，請在圖中畫出△A1B1C1，并寫出C1點坐標；
（2）圖中點A2（1，2）與點A關于直線l成軸對稱，請在圖中畫出直線l及△ABC關于直線l對稱的△A2B2C2，并寫出B2點坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知在以點O為圓心的兩個同心圓中，大圓的弦AB交小圓于點C，D（如圖）．
（1）求證：AC=BD；
（2）若大圓的半徑R=10，小圓的半徑r=8，且圓O到直線AB的距離為6，求AC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市為支援災區建設，計劃向
、
兩受災地運送急需物資分別為60噸和140噸，該市甲、乙兩地有急需物資分別為120噸和80噸，已知甲、乙兩地運到、兩地的每噸物資的運費如表所示：
甲 | 乙 | |
| 20元/噸 | 15元/噸 |
| 25元/噸 | 24元/噸 |
（1）設甲地運到地的急需物資為
噸，求總運費
（元）關于（噸）的函數關系式，并寫出的取值范圍；
（2）求最低總運費，并說明總運費最低時的運送方案．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com