
【題目】閱讀:點A、B在數軸上分別表示實數a、b,A、B兩點之間的距離表示為![]() ,當A、B兩點中有一點在原點時,不妨設點A在原點,如圖1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
,當A、B兩點中有一點在原點時,不妨設點A在原點,如圖1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
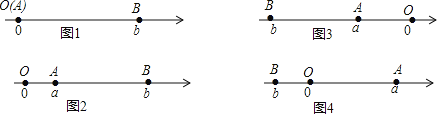
當A、B兩點都不在原點時,如圖2,點A、B都在原點的右邊∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;如圖3,點A、B都在原點的左邊,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;如圖4,點A、B在原點的兩邊,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= a +(-b)=∣a-b∣;
回答下列問題:
(1)數軸上表示3和5的兩點之間的距離是_________,數軸上表示-3和-5的兩點之間的距離是_________,數軸上表示1和-2的兩點之間的距離是 ;
(2)數軸上表示x和-1的兩點A和B之間的距離是 ,如果∣AB∣=3,那么x為 ;
(3)當代數式∣x+3∣+∣x-2∣取最小值時,相應的x的取值范圍是 ;當![]() 為 時,該代數式為7.
為 時,該代數式為7.
【答案】(1)2,2,3;(2)![]() ,2或-4;(3)
,2或-4;(3)![]() ,-4或3.
,-4或3.
【解析】
(1)(2)根據數軸上A、B兩點之間的距離![]() ,代入數值即可求出;
,代入數值即可求出;
(3)代數式![]() 的最小值,意思是數軸上數x到-3的距離與到2 的距離之和最小,據此即可求出x的范圍;若
的最小值,意思是數軸上數x到-3的距離與到2 的距離之和最小,據此即可求出x的范圍;若![]() ,在中間的時候代數式的值是5,只要在-3的左側和2的右側各找到一個到最近點距離為1的點就是所求.
,在中間的時候代數式的值是5,只要在-3的左側和2的右側各找到一個到最近點距離為1的點就是所求.
解:(1)數軸上表示3和5的兩點之間的距離是![]() ;
;
數軸上表示-3和-5的兩點之間的距離是![]() ;
;
數軸上表示1和-2的兩點之間的距離是![]() ;
;
(2)數軸上表示x和-1的兩點A和B之間的距離是![]() ;
;
如果![]() ,則
,則![]() ,所以
,所以![]() 或
或![]() ,解得:x=2或-4;
,解得:x=2或-4;
(3)代數式![]() 的最小值,意思是數軸上數x到-3的距離與到2 的距離之和最小,那么x應在-3與2之間的線段上,所以
的最小值,意思是數軸上數x到-3的距離與到2 的距離之和最小,那么x應在-3與2之間的線段上,所以![]() ,這個最小值是
,這個最小值是![]() ;
;
若![]() ,在
,在![]() 時,
時,![]() =5,所以只要在數軸上-3的左側和2的右側各找到一個到-3的距離和到2的距離為1的點就是所求,在數軸上-3的左側的數是-4,2的右側的數是3,所以當x=-4或3時,
=5,所以只要在數軸上-3的左側和2的右側各找到一個到-3的距離和到2的距離為1的點就是所求,在數軸上-3的左側的數是-4,2的右側的數是3,所以當x=-4或3時,![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】(1)如圖1,點![]() 在線段
在線段![]() 上,
上,![]() ,
,![]() ,點
,點![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 的中點.求線段
的中點.求線段![]() 的長;
的長;
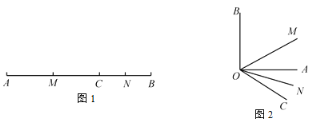
(2)點![]() 在線段
在線段![]() 上,若
上,若![]() ,點
,點![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 的中點.你能得出
的中點.你能得出![]() 的長度嗎?并說明理由.
的長度嗎?并說明理由.
(3)類似的,如圖2,![]() 是直角,射線
是直角,射線![]() 在
在![]() 外部,且
外部,且![]() 是銳角,
是銳角,![]() 是
是![]() 的平分線,
的平分線,![]() 是
是![]() 的平分線.當
的平分線.當![]() 的大小發生改變時,
的大小發生改變時,![]() 的大小也會發生改變嗎?為什么?
的大小也會發生改變嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數軸上![]() 、
、![]() 兩點分別表示有理數
兩點分別表示有理數![]() 和
和![]() ,我們用
,我們用![]() 表示
表示![]() 到
到![]() 之間的距離;例如
之間的距離;例如![]() 表示7到3之間的距離.
表示7到3之間的距離.
(1)當![]() 時,
時,![]() 的值為 .
的值為 .
(2)如何理解![]() 表示的含義?
表示的含義?
(3)若點![]() 、
、![]() 在0到3(含0和3)之間運動,求
在0到3(含0和3)之間運動,求![]() 的最小值和最大值.
的最小值和最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】騎共享單車已成為人們喜愛的一種綠色出行方式.已知A、B、C三家公司的共享單車都是按騎車時間收費,標準如下:
公司 | 單價(元/半小時) | 充值優惠 |
A | m | 充20元送5元,即:充20元實得25元 |
B | m-0.2 | 無 |
C | 1 | 充20元送20元,即:充20元實得40元 |
(注:使用這三家公司的共享單車,不足半小時均按半小時計費.用戶的賬戶余額長期有效,但不可提現.)
4月初,李明注冊成了A公司的用戶,張紅注冊成了B公司的用戶,并且兩人在各自賬戶上分別充值20元.一個月下來,李明、張紅兩人使用單車的次數恰好相同,且每次都在半小時以內,結果到月底李明、張紅的賬戶余額分別顯示為5元、8元.
(1)求m的值;
(2)5月份,C公司在原標準的基礎上又推出新優惠:每月的月初給用戶送出5張免費使用券(1
次用車只能使用1張券).如果王磊每月使用單車的次數相同,且在30次以內,每次用車都不超過
半小時. 若要在這三家公司中選擇一家并充值20元,僅從資費角度考慮,請你幫他作出選擇,并說
明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,直線l1經過(2,3)和(-1,-3):直線l2經過原點O,且與直線l1交于點P(-2,a).
(1)求a的值;
(2)(-2,a)可看成怎樣的二元一次方程組的解?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司購買了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的單價比
型芯片的單價比![]() 型芯片的單價少9元,已知該公司用3120元購買
型芯片的單價少9元,已知該公司用3120元購買![]() 型芯片的條數與用4200元購買
型芯片的條數與用4200元購買![]() 型芯片的條數相等.
型芯片的條數相等.
(1)求該公司購買的![]() 、
、![]() 型芯片的單價各是多少元?
型芯片的單價各是多少元?
(2)若兩種芯片共購買了200條,且購買的總費用為6280元,求購買了多少條![]() 型芯片?
型芯片?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=BC=4,AO=BO,P是射線CO上的一個動點,∠AOC=60°,則當△PAB為直角三角形時,AP的長為 __________________.
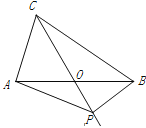
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某社區超市第一次用6000元購進甲、乙兩種商品,其中乙商品的件數比甲商品件數的![]() 倍多15件,甲、乙兩種商品的進價和售價如下表:(注:獲利=售價﹣進價)
倍多15件,甲、乙兩種商品的進價和售價如下表:(注:獲利=售價﹣進價)
甲 | 乙 | |
進價(元/件) | 22 | 30 |
售價(元/件) | 29 | 40 |
(1)該超市購進甲、乙兩種商品各多少件?
(2)該超市將第一次購進的甲、乙兩種商品全部賣完后一共可獲得多少利潤?
(3)該超市第二次以第一次的進價又購進甲、乙兩種商品,其中甲商品的件數不變,乙商品的件數是第一次的3倍;甲商品按原價銷售,乙商品打折銷售,第二次兩種商品都銷售完以后獲得的總利潤比第一次獲得的總利潤多180元,求第二次乙商品是按原價打幾折銷售?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級(1)班部分學生接受一次內容為“最適合自己的考前減壓方式”的調查活動,收集整理數據后,老師將減壓方式分為五類,并繪制了如圖①②兩幅不完整的統計圖,請根據圖中的信息解答下列問題.
(1)九年級(1)班接受調查的學生共有多少名?
(2)補全條形統計圖,并計算扇形統計圖中的“體育活動C”所對應的圓心角度數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com