
分析 (1)根據自變量與函數值的對應關系,可得A、C點的坐標,可得答案;
(2)①以A為直角頂點時,根據根據等腰三角形的性質,可得∠2的度數,∠3的度數,根據對頂角的性質,可得∠4的度數,根據等腰直角三角形的性質,可得P1H1=H1G,可得關于a的方程,根據解方程,可得a的值,再根據自變量與函數值的對應關系,可得答案;②當C為直角頂點時,根據角的和差,可得∠P2CH2=45°,根據等腰直角三角形的性質,可得關于a的方程,根據解方程,可得a的值,再根據自變量與函數值的對應關系,可得答案;
(3)根據矩形的性質,可得OD與EF的關系,根據垂線段的性質,可得OD的長,根據圓的面積公式.
解答 (1)證明:由拋物線y=x2+2x-3
令y=0,則x2+2x-3=0,解得x1=-3,x2=1,
所以A(-3,0),即OA=3;
令x=0,則y=-3,
所以C(0,-3),即OC=3;
所以OA=OC;
(2)解:①當A為直角頂點時,過點A作AP1⊥AC,交拋物線于點P1,交y軸于點G,過P1作P1H1⊥y軸于點H1,如圖1所示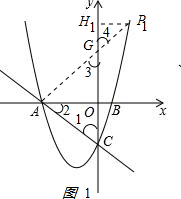 ,
,
由(1)OA=OC,∠AOC=90°
∴△AOC為等腰直角三角形,
∴∠1=∠2=45°.
∵∠P1AC=90°,
∴∠P1AO=45°,∠3=45°,
∴∠4=∠3=45°,
∴∠H1P1G=45°
△AOG,△P1H1G為等腰直角三角形
即OA=OG=3,P1H1=H1G,
設P1(a,a2+2a-3)
則 a=a2+2a-3-3,
解得a1=2,a2=-3(舍)
此時a2+2a-3=5
所以P1坐標是(2,5);
②當C為直角頂點時,過點C作CP2⊥AC,交拋物線于點P2,過P2作P2H2⊥y軸于點H2,如圖2所示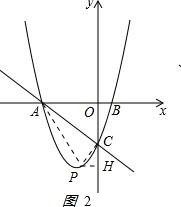 ,
,
∵∠1=45°,∠P2CA=90°,
∴∠P2CH2=45°.
∵∠P2H2C=90°,
∴△P2H2C為等腰直角三角形.
即P2H2=H2C
設P2(a,a2+2a-3)
則-a=-a2-2a+3-3,
解得a1=-1,a2=0(舍去),
此時a2+2a-3=-4
所以P2坐標是(-1,-4)
綜上所述,點P坐標是(2,5)或(-1,-4).
(3)△DEF的外接圓面積最小等于$\frac{9π}{8}$.
如圖3所示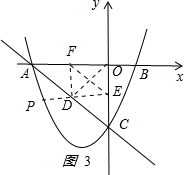 ,
,
因為△DEF為直角三角形,則它外接圓的直徑為線段EF,要使圓的面積最小,則直徑EF必須取最小值,
又因為EF與OD是矩形OEDF的對角線,所以EF=OD.
因為點到線的距離,垂線段最短,得
OD最小值=$\frac{3}{2}\sqrt{2}$,
故EF=$\frac{3}{2}\sqrt{2}$時,△DEF的外接圓面積最小,得
π($\frac{3\sqrt{2}}{2}$)2=$\frac{9π}{8}$,
△DEF的外接圓面積最小等于$\frac{9π}{8}$.
點評 本題考查了二次函數綜合題,利用自變量與函數值的對應關系得出A、C點的坐標是解題關鍵;利用等腰三角形的性質得出關于a的方程式解題關鍵,要分類討論,以防遺漏;利用矩形的性質得出OD與EF的關系是解題關鍵,又利用了垂線段的性質.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 名稱 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
| 圖形 | 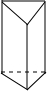 | 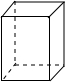 | 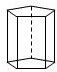 | 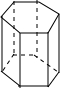 |
| 頂點數a | 6 | 8 | 10 | 12 |
| 棱數b | 9 | 12 | 15 | 18 |
| 面數c | 5 | 6 | 7 | 8 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
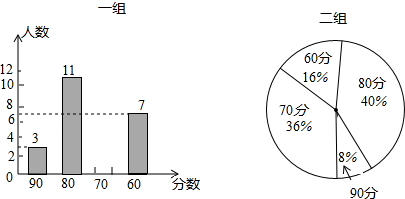
| 平均數 | 中位數 | 眾數 | 方差 | |
| 一組 | 74 | 80 | 80 | 104 |
| 二組 | 74 | 70 | 80 | 72 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com