
【題目】在新的教學改革的推動下,某中學初三年級積極推進走班制教學.為了了解一段時間以來“至善班”的學習效果,年級組織了多次定時測試,現隨機選取甲、乙兩個“至善班”,從中各抽取20名同學在某一次定時測試中的數學成績,其結果記錄如下:
收集數據:
“至善班”甲班的20名同學的數學成績統計(滿分為100分)(單位:分):86 90 60 76 92 83 56 76 85 70 96 96 90 68 78 80 68 96 85 81
“至善班”乙班的20名同學的數學成績統計(滿分為100分)(單位:分):78 96 75 76 82 87 60 54 87 72 100 82 78 86 70 92 76 80 98 78
整理數據:(成績得分用x表示)
分數 數量 班級 | 0≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班(人數) | 1 | 3 | 4 | 6 | 6 |
乙班(人數) | 1 | 1 | 8 | 6 | 4 |
分析數據,并回答下列問題:
(1)完成下表:
平均數 | 中位數 | 眾數 | |
甲班 | 80.6 | 82 | a= |
乙班 | 80.35 | b= | 78 |
(2)在“至善班”甲班的扇形圖中,成績在70≤x<80的扇形中,所對的圓心角α的度數為 ,估計全部“至善班”的1600人中優秀人數為 人.(成績大于等于80分為優秀)
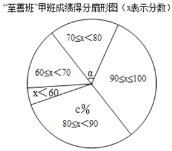
(3)根據以上數據,你認為“至善班” 班(填“甲”或“乙”)所選取做樣本的同學的學習效果更好一些,你所做判斷的理由是:① ;② .
【答案】(1)96,79;(2)72°,880;(3)甲,甲的優秀率高,甲的中位數比乙的中位數大
【解析】
(1)根據眾數,中位數的定義即可解決問題;
(2)根據圓心角=360°×百分比計算即可,利用樣本估計總體的思想解決問題;
(3)根據優秀率,中位數,平均數的大小即可判斷。答案不唯一,合理即可.
解:(1)將甲班成績重新整理如下:
56 60 68 68 70 76 76 78 80 81 83 85 85 86 90 90 92 96 96 96,
其中96出現次數做多,
∴眾數a=96(分),
將乙班成績重新整理如下:
54 60 70 72 75 76 76 78 78 78 80 82 82 86 87 87 92 96 98 100,
其中中位數b![]() 79(分),
79(分),
故答案為:96,79;
(2)成績在70≤x<80的扇形中,所對的圓心角α的度數為360°![]() 72°,
72°,
估計全部“至善班”的1600人中優秀人數為1600![]() 880(人).
880(人).
(3)甲所選取做樣本的同學的學習效果更好一些,你所做判斷的理由是:甲的優秀率高,甲的中位數比乙的中位數大,
故答案為:甲,甲的優秀率高,甲的中位數比乙的中位數大.


科目:初中數學 來源: 題型:
【題目】圖![]() 、圖
、圖![]() 分別是
分別是![]() 的網格,網格中的每個小正方形的邊長均為1,點
的網格,網格中的每個小正方形的邊長均為1,點![]() 、
、![]() 、
、![]() 、
、![]() 在小正方形的頂點上.請在網格中按要求畫出圖形:
在小正方形的頂點上.請在網格中按要求畫出圖形:
(1)在圖![]() 中畫以
中畫以![]() 為斜邊的直角三角形
為斜邊的直角三角形![]() (點
(點![]() 在小正方形的頂點上),使得
在小正方形的頂點上),使得![]() ;
;
(2)在圖![]() 中畫以
中畫以![]() 為邊的四邊形
為邊的四邊形![]() (點
(點![]() 、
、![]() 在小正方形的頂點上),使得四邊形
在小正方形的頂點上),使得四邊形![]() 是中心對稱圖形但不是軸對稱圖形,且
是中心對稱圖形但不是軸對稱圖形,且![]() ,并直接寫出四邊形
,并直接寫出四邊形![]() 的面積.
的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的正方形組成的網格中建立直角坐標系,△AOB的頂點均在格點上,點O為原點,點A、B的坐標分別是A(3,2)、B(1,3).

(1)將△AOB向下平移3個單位后得到△A1O1B1,則點B1的坐標為 ;
(2)將△AOB繞點O逆時針旋轉90°后得到△A2OB2,請在圖中作出△A2OB2,并求出這時點A2的坐標為 ;
(3)在(2)中的旋轉過程中,線段OA掃過的圖形的面積 .
查看答案和解析>>
科目:初中數學 來源: 題型:
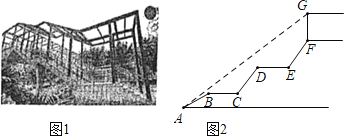
【題目】為了方便學生在上下學期間安全過馬路,南岸區政府決定在南開(融僑)中學校門口修建人行天橋(如圖1),其平面圖如圖2所示,初三(8)班的學生小劉想利用所學知識測量天橋頂棚距地面的高度.天橋入口A點有一臺階AB=2m,其坡角為30°,在AB上方有兩段平層BC=DE=1.5m,且BC,DE與地面平行,BC,DE上方又緊接臺階CD,EF,其長度相等且坡度均為i=4:3,頂棚距天橋距離FG=2m,且小劉從入口A點測得頂棚頂端G的仰角為37°,請根據以上數據,幫小劉計算出頂端G點距地面高度為( )m.(結果保留一位小數,參考數據:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在開展“經典閱讀”活動中,某學校為了解全校學生利用課外時間閱讀的情況,學校團委隨機抽取若干名學生,調查他們一周的課外閱讀時間,并根據調查結果繪制了如下尚不完整的統計表.根據圖表信息,解答下列問題:
頻率分布表
閱讀時間(小時) | 頻數(人) | 頻率 |
| 6 | 0.12 |
|
| 0.24 |
| 15 | 0.3 |
| 12 |
|
| 5 | 0.1 |
合計 |
| 1 |
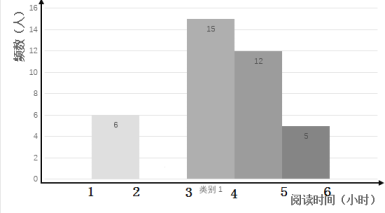
(1)求![]() __________,
__________,![]() _________;
_________;
(2)將頻數分布直方圖補充完整(畫圖后請標注相應的頻數);
(3)在![]() 范圍內的5名同學中恰好有2名男生和3名女生,現從中隨機挑選2名同學代表學校參加全市經典閱讀比賽,請用樹狀圖法或者列表法求出恰好選中“1男1女”的概率.
范圍內的5名同學中恰好有2名男生和3名女生,現從中隨機挑選2名同學代表學校參加全市經典閱讀比賽,請用樹狀圖法或者列表法求出恰好選中“1男1女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,∠B=120°,AB與CD之間的距離是![]() ,AB=28,在AB上取一點E(AE<BE),使得∠DEC=120°,則AE=_____.
,AB=28,在AB上取一點E(AE<BE),使得∠DEC=120°,則AE=_____.
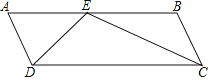
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=2,∠DAB=60°,點E是AD邊的中點,點M是AB邊上的一個動點(不與點A重合),延長ME交CD的延長線于點N,連接MD,AN.
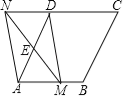
(1)求證:四邊形AMDN是平行四邊形.
(2)當AM的值為何值時,四邊形AMDN是矩形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著《流浪地球》的熱播,其同名科幻小說的銷量也急劇上升.為應對這種變化,某網店分別花20000元和30000元先后兩次增購該小說,第二次的數量比第一次多500套,且兩次進價相同.
(1)該科幻小說第一次購進多少套?
(2)根據以往經驗:當銷售單價是25元時,每天的銷售量是250套;銷售單價每上漲1元,每天的銷售量就減少10套.網店要求每套書的利潤不低于10元且不高于18元.
①直接寫出網店銷售該科幻小說每天的銷售量y(套)與銷售單價x(元)之間的函數關系式及自變量x的取值范圍;
②網店決定每銷售1套該科幻小說,就捐贈a(0<a<7)元給困難職工,每天扣除捐贈后可獲得的最大利潤為1960元,求a的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com