
分析 題中只說明是等腰三角形沒有指明是銳角三角形還是鈍角三角形,所以應該分兩情況進行分析.
解答 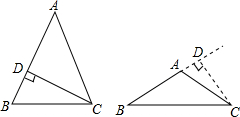 解:①如圖,△ABC中,AB=AC,CD⊥AB,
解:①如圖,△ABC中,AB=AC,CD⊥AB,
∵△ABC中,CD⊥AB且CD=2$\sqrt{3}$,AB=4,AB=AC,
∴sinA=$\frac{CD}{AC}$=$\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$,
∴∠A=60°.
②如圖,△ABC中,AB=AC,CD⊥BA的延長線于點D,
∵△ABC中,CD⊥AB且CD=2$\sqrt{3}$,AB=4,AB=AC,
∴sin∠DAC=$\frac{CD}{AC}$=$\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$,
∴∠DAC=60°,
∴∠BAC=120°.
故答案為:60°或120°.
點評 本題考查了直角三角形的性質以及等腰三角形的性質,解題時要認真審題,弄清題意是關鍵,此題難度不大,易于理解.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:解答題
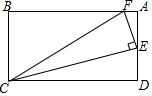 已知,如圖,在矩形ABC中.E是AD的中點,EF⊥EC交AB于點F,連FC(AB>AE),求證:$\frac{DE}{AB}$=$\frac{AF}{DE}$.
已知,如圖,在矩形ABC中.E是AD的中點,EF⊥EC交AB于點F,連FC(AB>AE),求證:$\frac{DE}{AB}$=$\frac{AF}{DE}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 4 | 6 | 8 | 10 | … | 2n | … |
| 3 | 8 | 15 | 24 | … | … | |
| 5 | 10 | 17 | 26 | … | … |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com