
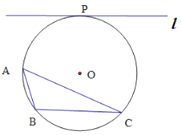
【題目】已知⊙O為△ABC的外接圓,直線l與⊙O相切于點P,且![]() ∥BC.
∥BC.
(1) 連接PO,并延長交⊙O于點D,連接AD.證明: AD平分∠BAC;
(2) 在(1)的條件下,AD交BC于點E,連接CD.若DE=2,AE=6.試求CD的長.
【答案】(1)證明見解析;(2)CD=4.
【解析】試題分析:(1)由切線的性質得到PD⊥l,再由![]() ∥BC,得到PD垂直平分弦BC,由垂徑定理得到弧BD=弧DC,即可得到結論;
∥BC,得到PD垂直平分弦BC,由垂徑定理得到弧BD=弧DC,即可得到結論;
(2)證明△ADC∽△CDE,由相似三角形的對應邊成比例即可得到結論.
試題解析:解:(1)∵![]() 與⊙O相切于點P,∴PD⊥l.∵
與⊙O相切于點P,∴PD⊥l.∵ ![]() ∥BC,∴PD⊥BC,∴ PD平分弦BC ,∴弧BD=弧DC , ∴∠BAD=∠DAC ,即AD平分∠BAC;
∥BC,∴PD⊥BC,∴ PD平分弦BC ,∴弧BD=弧DC , ∴∠BAD=∠DAC ,即AD平分∠BAC;
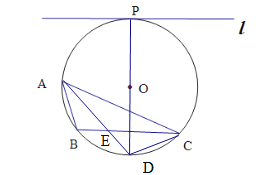
(2)∠BAD=∠BCD且∠BAD=∠DAC,∴ ∠DAC=∠BCD.
在△ADC和△CDE中
∵∠DAC=∠BCD,∠ADC=∠EDC,∴△ADC∽△CDE ,
∴![]() ,
, ![]() ,∴DC=4.
,∴DC=4.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某小區有兩段長度相等的道路需硬化,現分別由甲、乙兩個工程隊同時開始施工.如圖的線段和折線是兩隊前6天硬化的道路長y甲、y乙(米)與施工時間x(天)之間的函數圖象

根據圖象解答下列問題:
(1)直接寫出y甲、y乙(米)與x(天)之間的函數關系式.
①當0<x≤6時,y甲= ;
②當0<x≤2時,y乙= ;當2<x≤6時,y乙= ;
(2)求圖中點M的坐標,并說明M的橫、縱坐標表示的實際意義;
(3)施工過程中,甲隊的施工速度始終不變,而乙隊在施工6天后,每天的施工速度提高到120米/天,預計兩隊將同時完成任務.兩隊還需要多少天完成任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了調查學生對“節約教育”內容的了解程度(程度分為:“![]() —了解很多”,“
—了解很多”,“![]() —了解較多”,“
—了解較多”,“![]() —了解較少”,“
—了解較少”,“![]() —不了解”),對某中學的部分學生進行了調查,將這次調查的結果繪制成以下兩幅統計圖.根據以上信息,解答下列問顧:
—不了解”),對某中學的部分學生進行了調查,將這次調查的結果繪制成以下兩幅統計圖.根據以上信息,解答下列問顧:
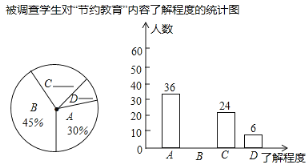
(1)本次調查了多少名學生?
(2)若該校共有1800名學生,請你估計這所學校的所有學生中,對“節約教育”內容“了解較多”的有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
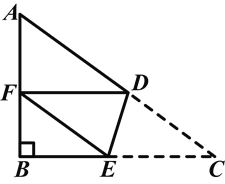
【題目】如圖,在△ABC中,∠B=90°,AB=6,BC=8,將△ABC沿DE折疊,使點C落在AB邊上的點F處,并且FD∥BC,則CD的長是( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,鐘表的分針勻速旋轉一周需要60分鐘,那么:
(1)它的旋轉中心是什么?
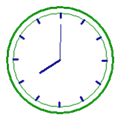
(2)分針旋轉一周,時針旋轉多少度?
(3)上午8點整,時針和分針的夾角是多少?8點半呢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新型冠狀病毒肺炎疫情發生后,全社會積極參與疫情防控工作,某市為了盡快完成100萬只口罩的生產任務,安排甲、乙兩個大型工廠完成.已知甲廠每天能生產口罩的數量是乙廠每天能生產口罩的數量的1.5倍,并且在獨立完成60萬只口罩的生產任務時,甲廠比乙廠少用5天.問至少應安排兩個工廠工作多少天才能完成任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O是坐標原點,矩形OABC的頂點A,C分別在坐標軸上,點B的坐標為(4,2).直線![]() 分別交AB,BC于點M,N,反比例函數
分別交AB,BC于點M,N,反比例函數![]() 的圖像經過點M.
的圖像經過點M.
(1)求反比例函數的解析式;
(2)判斷點N是否在反比例函數![]() 的圖像上?試說明理由.
的圖像上?試說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把一個轉盤分成六等份,依次標上數字1、2、3、4、5、6,小明和小芳分別只轉動一次轉盤.小明同學先轉動轉盤,結果指針指向2,接下來小芳轉動轉盤,若把小明和小芳轉動轉盤指針指向的數字分別記作![]() 、
、![]() ,把
,把![]() 、
、![]() 作為點
作為點![]() 的橫、縱坐標.
的橫、縱坐標.
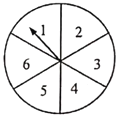
(1)寫出點![]() 所有可能的坐標;
所有可能的坐標;
(2)求點![]() 在直線
在直線![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A、B在反比例函數y=![]() 的圖象上,過點A、B作x軸的垂線,垂足分別是M、N,射線AB交x軸于點C,若OM=MN=NC,四邊形AMNB的面積是3,則k的值為( )
的圖象上,過點A、B作x軸的垂線,垂足分別是M、N,射線AB交x軸于點C,若OM=MN=NC,四邊形AMNB的面積是3,則k的值為( )
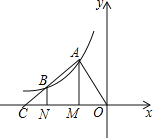
A.2 B.4 C.﹣2 D.﹣4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com