
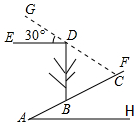
 如圖,斜坡AF的坡度為5:12,斜坡AF上一棵與水平面垂直的大樹BD在陽光照射下,在斜坡上的影長BC=6.5米,此時光線與水平線恰好成30°角,求大樹BD的高.(結果精確的0.1米,參考數據$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如圖,斜坡AF的坡度為5:12,斜坡AF上一棵與水平面垂直的大樹BD在陽光照射下,在斜坡上的影長BC=6.5米,此時光線與水平線恰好成30°角,求大樹BD的高.(結果精確的0.1米,參考數據$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 分析 作CM⊥DB于點M,已知BC的坡度即可得到BM和CM的比值,則在直角△MBC中,利用勾股定理即可求得BM和MC的長度,然后在直角△DCM中利用三角函數求得DM的長,則BD=BM+DM,據此即可求解.
解答  解:作CM⊥DB于點M,
解:作CM⊥DB于點M,
∵斜坡AF的坡度是1::2.4,∠A=∠BCM,
∴$\frac{BM}{CM}$=$\frac{1}{2.4}$=$\frac{5}{12}$,
∴在直角△MBC中,設BM=5x,則CM=12x.
由勾股定理可得:BM2+CM2=BC2,
∴(5x)2+(12x)2=6.52,
解得:x=$\frac{1}{2}$,
∴BM=5x=$\frac{5}{2}$,CM=12x=6,
在直角△MDC中,∠DCM=∠EDG=30°,
∴DM=CM•tan∠DCM=6tan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$,
∴BD=DM+BM=$\frac{5}{2}$+2$\sqrt{3}$≈2.5+2×1.732≈6.0(米).
答:大樹的高約為6.0米.
點評 本題考查了解直角三角形的應用,兩個直角三角形有公共的直角邊,先求出公共邊的長度是解決此類題目的基本出發點.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com