
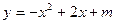 的圖象與x軸相交于A、B兩點(A
的圖象與x軸相交于A、B兩點(A ,求點B的坐標;
,求點B的坐標;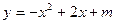 的圖象與x軸相交于A、B兩點
的圖象與x軸相交于A、B兩點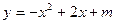 的圖象的對稱軸為直線x=-
的圖象的對稱軸為直線x=-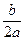 =1························· 4分
=1························· 4分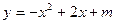 中得m="15···············································" 4分
中得m="15···············································" 4分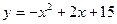
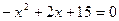 ········································································ 5分
········································································ 5分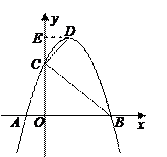
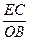 =
= .····························································· 7分
.····························································· 7分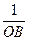 =
=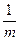 .
.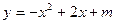 得:-m 2+2 m + m=0.
得:-m 2+2 m + m=0.

 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
查看答案和解析>>
科目:初中數學 來源: 題型:
 已知二次函數的圖象與x軸交于點A(-1,0)和點B(3,0),且與直線y=kx-4交y軸于點C.
已知二次函數的圖象與x軸交于點A(-1,0)和點B(3,0),且與直線y=kx-4交y軸于點C. 查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com