
【題目】如圖,已知拋物線y=﹣x2+ax+3的頂點為P,它分別與x軸的負半軸、正半軸交于點A,B,與y軸正半軸交于點C,連接AC,BC,若tan∠OCB﹣tan∠OCA=![]() .
.
(1)求a的值;
(2)若過點P的直線l把四邊形ABPC分為兩部分,它們的面積比為1:2,求該直線的解析式.

【答案】(1)2;(2)y=﹣8x+12或y=4x
【解析】
(1)根據拋物線與坐標軸的交點可得一元二次方程,根據韋達定理可得x1+x2=a;由函數解析式可知當x=0時y的值,則可得OC的長;結合tan∠OCB﹣tan∠OCA=![]() 得出OB﹣OA=2,再用x1、x2表示出來,可得a的值;
得出OB﹣OA=2,再用x1、x2表示出來,可得a的值;
(2)由(1)可得拋物線的解析式,則可求得點P和點A、點B的坐標,延長PC交x軸于點D,作PF⊥x軸于點F,根據S四邊形ABPC=S△PDB﹣S△CDA,可求得四邊形ABPC的面積;設直線l與x軸交于點M(m,0),則BM=3﹣m,根據直線l把四邊形ABPC分為面積比為1:2的兩部分,分情況列出關于m的方程,解得m的值,則根據待定系數法可得直線l的解析式.
1)∵拋物線y=﹣x2+ax+3與x軸交于點A,B,
∴方程﹣x2+ax+3=0有兩個不同的實數根.
設這兩個根分別為x1、x2,且x1<0,x2>0,
由韋達定理得:x1+x2=a,
∵當x=0時,y=﹣x2+ax+3=3,
∴OC=3.
∵tan∠OCB﹣tan∠OCA=![]() .
.
∴![]() ﹣
﹣![]() =
=![]() ,
,
∴OB﹣OA=2,
∴x2﹣(﹣x1)=2,即x2+x1=2,
∴a=2.
(2)由(1)得拋物線的解析式為y=﹣x2+2x+3,
∴其頂點坐標為P(1,4).
解方程﹣x2+2x+3=0,得x1=﹣1、x2=3,
∴A(﹣1,0),B(3,0).
延長PC交x軸于點D,作PF⊥x軸于點F,
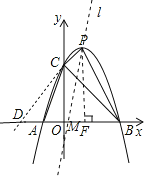
∴S四邊形ABPC=S△PDB﹣S△CDA
=![]() DBPF﹣
DBPF﹣![]() DAOC
DAOC
=![]() (3+3)×4﹣
(3+3)×4﹣![]() (3﹣1)×3
(3﹣1)×3
=9.
設直線l與x軸交于點M/span>(m,0),則BM=3﹣m,
∴S△PMB=![]() ×(3﹣m)×4=6﹣2m,
×(3﹣m)×4=6﹣2m,
當6﹣2m=![]() ×9=3時,m=
×9=3時,m=![]() ,此時M(
,此時M(![]() ,0),
,0),
即直線l過點P(1,4),M(![]() ,0),
,0),
由待定系數法可得l的解析式為y=﹣8x+12;
同理,當6﹣2m=![]() ×9=6時,m=0,此時M(0,0),即直線l過點P(1,4),M(0,0),
×9=6時,m=0,此時M(0,0),即直線l過點P(1,4),M(0,0),
由待定系數法可得l的解析式為y=4x;
綜上所述,直線l的解析式為y=﹣8x+12或y=4x.


 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:
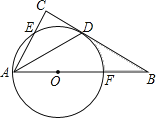
【題目】如圖,在△ABC中,∠C=90°,∠BAC的平分線交BC于點D,點O在AB上,以點O為圓心,OA為半徑的圓恰好經過點D,分別交AC,AB于點E,F.
(1)試判斷直線BC與⊙O的位置關系,并說明理由;
(2)若BD=2![]() ,BF=2,求陰影部分的面積(結果保留π).
,BF=2,求陰影部分的面積(結果保留π).
查看答案和解析>>
科目:初中數學 來源: 題型:
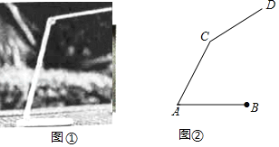
【題目】圖①是放置在水平面上的臺燈,圖②是其側面示意圖(臺燈底座高度忽略不計),其中燈臂AC=44cm,燈罩CD=32cm,燈臂與底座構成的∠CAB=60°.CD可以繞點C上下調節一定的角度.使用發現:當CD與水平線所成的角為30°時,臺燈光線最佳.現測得點D到桌面的距離為54.06cm.請通過計算說明此時臺燈光線是否為最佳?(參考數據:![]() 取1.73).
取1.73).
查看答案和解析>>
科目:初中數學 來源: 題型:
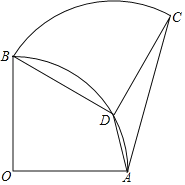
【題目】如圖,扇形OAB中,∠AOB=90°,將扇形OAB繞點B逆時針旋轉,得到扇形BDC,若點O剛好落在弧AB上的點D處,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在△ABC中,∠A=30°,點P從點A出發以2cm/s的速度沿折線A﹣C﹣B運動,點Q從點A出發以a(cm/s)的速度沿AB運動,P,Q兩點同時出發,當某一點運動到點B時,兩點同時停止運動.設運動時間為x(s),△APQ的面積為y(cm2),y關于x的函數圖象由C1,C2兩段組成,如圖2所示.
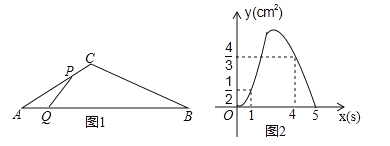
(1)求a的值;
(2)求圖2中圖象C2段的函數表達式;
(3)當點P運動到線段BC上某一段時△APQ的面積,大于當點P在線段AC上任意一點時△APQ的面積,求x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為緩解交通壓力,建設美麗遵義,市政府加快了風新快線的建設.如圖,A、B兩地之間有一座山,汽車原來從A地到B地需途徑C地沿折線ACB行駛,現開通隧道后,汽車可直接沿直線AB行駛.已知BC=8千米,∠A=45°,∠B=30°.
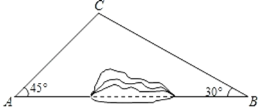
(1)開通隧道前,汽車從A地到B地大約要走多少千米?
(2)開通隧道后,汽車從A地到B地大約可以少走多少千米?(結果精確到0.1千米)(參考數據:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點P(![]() ,
,![]() )和直線y=kx+b,則點P到直線y=kx+b的距離證明可用公式d=
)和直線y=kx+b,則點P到直線y=kx+b的距離證明可用公式d=![]() 計算.
計算.
例如:求點P(﹣1,2)到直線y=3x+7的距離.
解:因為直線y=3x+7,其中k=3,b=7.
所以點P(﹣1,2)到直線y=3x+7的距離為:d=![]() =
=![]() =
=![]() =
=![]() .
.
根據以上材料,解答下列問題:
(1)求點P(1,﹣1)到直線y=x﹣1的距離;
(2)已知⊙Q的圓心Q坐標為(0,5),半徑r為2,判斷⊙Q與直線y=![]() x+9的位置關系并說明理由;
x+9的位置關系并說明理由;
(3)已知直線y=﹣2x+4與y=﹣2x﹣6平行,求這兩條直線之間的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,過點C的直線MN∥AB,D為AB邊上中點,過點D作DE⊥BC,交直線MN于E,垂足為F,連接CD、BE.
(1)求證:DF=![]() AC
AC
(2)試判斷四邊形BECD是什么特殊四邊形?說明你的理由;
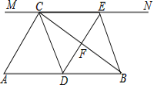
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com