
已知邊長為3的正方形ABCD中,點E在射線BC上,且BE=2CE,連結AE交射線DC于點F,將△ABE沿直線AE翻折,點B落在點B1處.
(1)如圖1,若點E在線段BC上,求CF的長;
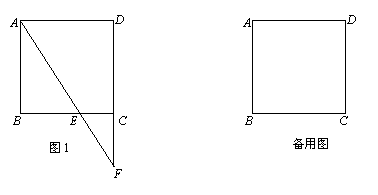 (2)求sin∠DAB1的值.
(2)求sin∠DAB1的值.
(1)CF=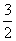 ………………………………………………………………… (1分)
………………………………………………………………… (1分)
(2)如圖1,延長AB1與DC交于點M,先證A M=FM……………………………… (2分)
M=FM……………………………… (2分)
設DM=x,則AM=FM=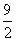 -x,在Rt△ADM中,(
-x,在Rt△ADM中,(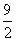 -x)2-x2=32…………… (3分)
-x)2-x2=32…………… (3分)
解得x=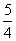 ,∴sin∠DAB1=
,∴sin∠DAB1=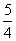 ÷(
÷(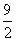 -
-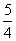 )=
)=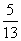 ………………………………………… (4分)
………………………………………… (4分)
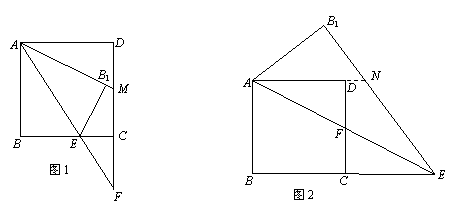
如圖2,當點E在BC的延長線上時,延長AD交B1E于點N,證AN=EN……(5分)
設B1N=y,則AN=EN=6-y,在Rt△AB1N中,(6-y)2-y2=32……………… (6分)
解得y=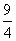 ,∴sin∠DAB1=
,∴sin∠DAB1=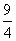 ÷(6-
÷(6-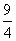 )=
)= ………………………………………… (8分)
………………………………………… (8分)


科目:初中數學 來源: 題型:
某校數學興趣 小組成員小華對本班上學期期末考試數學成績(成績取整數,滿分為100分)作了統計分析.請你根據圖表提供的信息,解答下列問題:
| 分組 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合計 |
| 頻數 | 2 | 8 | 20 | 16 | b | c |
| 頻率 | 0.04 | 0.16 | 0.40 | a | 0.08 | d |
(1)表中a= ,b= ,c= ,d= ;
(2)根據學校規定將有40%的學生參加校級數學冬令營活動,試確定參賽學生的最低資格線?
(2)數學老師準備從不低于90分的學生中選2人介紹學習經驗,其中符合條件的小華、小麗同時被選中的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
已知某廠現有A種金屬70噸,B種金屬52噸,現計劃用這兩種金屬生產M、N兩種型號的合金產品共80000套,已知做一套M型號的合金產品需要A種金屬0.6kg,B種金屬0.9kg,可獲利潤45元;做一套N型號的合金產品需要A種金屬1.1kg,B種金屬0.4kg,可獲利潤50元.若設生產N種型號的合金產品套數為x,用這批金屬生產這兩種型號的合金產品所獲總利潤為y元.
(1)求y與x的函數關系式,并求出自變量x的取值范圍;
(2)在生產這批合金產品時,N型號的合金產品應生產多少套,該廠所獲利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com