
【題目】某工廠生產部門為了解本部門工人的生產能力情況,進行了抽樣調查.該部門隨機抽取了30名工人某天每人加工零件的個數,數據如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面數據,得到條形統計圖:
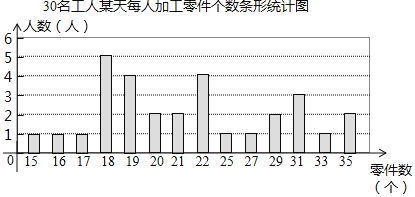
樣本數據的平均數、眾數、中位數如下表所示:
統計量 | 平均數 | 眾數 | 中位數 |
數值 | 23 | m | 21 |
根據以上信息,解答下列問題:
(1)上表中眾數m的值為 ;
(2)為調動工人的積極性,該部門根據工人每天加工零件的個數制定了獎勵標準,凡達到或超過這個標準的工人將獲得獎勵.如果想讓一半左右的工人能獲獎,應根據 來確定獎勵標準比較合適.(填“平均數”、“眾數”或“中位數”)
(3)該部門規定:每天加工零件的個數達到或超過25個的工人為生產能手.若該部門有300名工人,試估計該部門生產能手的人數.
 名題金卷系列答案
名題金卷系列答案 優加精卷系列答案
優加精卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,![]() 是半圓
是半圓![]() 的直徑,
的直徑,![]() 、
、![]() 、
、![]() 是半圓的四等分點,
是半圓的四等分點,![]() 于
于![]() ,連接
,連接![]() 、
、![]() 相交于
相交于![]() 點,連接
點,連接![]() 、
、![]() ,下列結論:①
,下列結論:①![]() ;②
;②![]() ;③
;③![]() ,其中正確的結論是( )
,其中正確的結論是( )
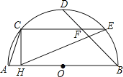
A. ①②③ B. 只有①② C. 只有①③ D. 只有③
查看答案和解析>>
科目:初中數學 來源: 題型:
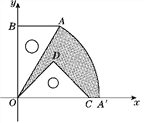
【題目】如圖,有一塊含30°角的直角三角板OAB的直角邊BO的長恰與另一塊等腰直角三角板ODC的斜邊OC的長相等,把這兩塊三角板放置在平面直角坐標系中,且OB=3![]() .
.
(1)若某反比例函數的圖象的一個分支恰好經過點A,求這個反比例函數的解析式;
(2)若把含30°角的直角三角板繞點O按順時針方向旋轉后,斜邊OA恰好落在x軸上,點A落在點A′處,試求圖中陰影部分的面積.(結果保留π)
【答案】(1)反比例函數的解析式為y=![]() ;(2)S陰影=6π-
;(2)S陰影=6π-![]() .
.
【解析】分析:(1)根據tan30°=![]() ,求出AB,進而求出OA,得出A的坐標,設過A的雙曲線的解析式是y=
,求出AB,進而求出OA,得出A的坐標,設過A的雙曲線的解析式是y=![]() ,把A的坐標代入求出即可;(2)求出∠AOA′,根據扇形的面積公式求出扇形AOA′的面積,求出OD、DC長,求出△ODC的面積,相減即可求出答案.
,把A的坐標代入求出即可;(2)求出∠AOA′,根據扇形的面積公式求出扇形AOA′的面積,求出OD、DC長,求出△ODC的面積,相減即可求出答案.
本題解析:
(1)在Rt△OBA中,∠AOB=30°,OB=3![]() ,
,
∴AB=OB·tan 30°=3.
∴點A的坐標為(3,3![]() ).
).
設反比例函數的解析式為y=![]() (k≠0),
(k≠0),
∴3![]() =
=![]() ,∴k=9
,∴k=9![]() ,則這個反比例函數的解析式為y=
,則這個反比例函數的解析式為y=![]() .
.
(2)在Rt△OBA中,∠AOB=30°,AB=3,
sin ∠AOB=![]() ,即sin 30°=
,即sin 30°=![]() ,
,
∴OA=6.
由題意得:∠AOC=60°,S扇形AOA′=![]() =6π.
=6π.
在Rt△OCD中,∠DOC=45°,OC=OB=3![]() ,
,
∴OD=OC·cos 45°=3![]() ×
×![]() =
=![]() .
.
∴S△ODC=![]() OD2=
OD2=![]()
![]() =
=![]() .
.
∴S陰影=S扇形AOA′-S△ODC=6π-![]() .
.
點睛:本題考查了勾股定理、待定系數法求函數解析式、特殊角的三角函數值、扇形的面積及等腰三角形的性質,本題屬于中檔題,難度不大,將不規則的圖形的面積表示成多個規則圖形的面積之和是解答本題的關鍵.
【題型】解答題
【結束】
26
【題目】矩形ABCD一條邊AD=8,將矩形ABCD折疊,使得點B落在CD邊上的點P處.
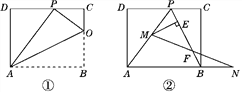
(1)如圖①,已知折痕與邊BC交于點O,連接AP,OP,OA.
① 求證:△OCP∽△PDA;
② 若△OCP與△PDA的面積比為1:4,求邊AB的長.
(2)如圖②,在(1)的條件下,擦去AO和OP,連接BP.動點M在線段AP上(不與點P,A重合),動點N在線段AB的延長線上,且BN=PM,連接MN交PB于點F,作ME⊥BP于點E.試問動點M,N在移動的過程中,線段EF的長度是否發生變化?若不變,求出線段EF的長度;若變化,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店準備購進一批電冰箱和空調,每臺電冰箱的進價比每臺空調的進價多400元,商店用8000元購進電冰箱的數量與用6400元購進空調的數量相等.
(1)求每臺電冰箱與空調的進價分別是多少?
(2)已知電冰箱的銷售價為每臺2100元,空調的銷售價為每臺1750元.若商店準備購進這兩種家電共100臺,其中購進電冰箱x臺(33≤x≤40),那么該商店要獲得最大利潤應如何進貨?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分10分)如圖,直線y=﹣![]() x+6分別與x軸、y軸交于A、B兩點;直線y=
x+6分別與x軸、y軸交于A、B兩點;直線y=![]() x與AB交于點C,與過點A且平行于y軸的直線交于點D.點E從點A出發,以每秒1個單位的速度沿x軸向左運動.過點E作x軸的垂線,分別交直線AB、OD于P、Q兩點,以PQ為邊向右作正方形PQMN.設正方形PQMN與△ACD重疊部分(陰影部分)的面積為S(平方單位),點E的運動時間為t(秒).
x與AB交于點C,與過點A且平行于y軸的直線交于點D.點E從點A出發,以每秒1個單位的速度沿x軸向左運動.過點E作x軸的垂線,分別交直線AB、OD于P、Q兩點,以PQ為邊向右作正方形PQMN.設正方形PQMN與△ACD重疊部分(陰影部分)的面積為S(平方單位),點E的運動時間為t(秒).

(1)求點C的坐標.
(2)當0<t<5時,求S與t之間的函數關系式,并求S的最大值。
(3)當t>0時,直接寫出點(5,3)在正方形PQMN內部時t的取值范圍。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在 4 4 的正方形網格中,有 5 個黑色小正方形.
(1)請你移動一個黑色小正方形,使移動后所形成的4 4 的正方形網格圖形是軸對稱圖形.如:將 8 號小正方形移至 14 號;你的另一種做法是將 號小正方形移至 號(填寫標號即可);
(2)請你移動 2 個小正方形,使移動后所形成的圖形是軸對稱圖形.你的一種做法是將 號小正方形移至 號、將 號小正方形移至 號(填寫標號即可).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC 中,AB=AC,CD是∠ACB的平分線,DE∥BC,交AC于點 E.
(1)求證:DE=CE.
(2)若∠CDE=35°,求∠A 的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形OABC中,O為平面直角坐標系的原點,A點的坐標為![]() ,C點的坐標為
,C點的坐標為![]() ,點B在第一象限內,點P從原點出發,以每秒2個單位長度的速度沿著
,點B在第一象限內,點P從原點出發,以每秒2個單位長度的速度沿著![]() 的路線移動
的路線移動![]() 即:沿著長方形移動一周
即:沿著長方形移動一周![]() .
.
![]() 寫出點B的坐標
寫出點B的坐標![]() ______
______![]()
![]() 當點P移動了4秒時,描出此時P點的位置,并求出點P的坐標.
當點P移動了4秒時,描出此時P點的位置,并求出點P的坐標.
![]() 在移動過程中,當點P到x軸距離為5個單位長度時,求點P移動的時間.
在移動過程中,當點P到x軸距離為5個單位長度時,求點P移動的時間.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com