
【題目】某市水費采用階梯收費制度,即:每月用水不超過15噸時,每噸需繳納水費a元,每月用水量超過15噸時,超過15噸的部分按每噸提高b元繳納下表是嘉琪家一至四月份用水量和繳納水費情況.根據表格提供的數據,回答:
月份 | 一 | 二 | 三 | 四 |
月用水量(噸) | 14 | 18 | 16 | 13 |
水費(元) | 42 | 60 | 50 | 39 |
(1)a= 元;b= 元;
(2)求月繳納水費p(元)與月用水量t(噸)之間的函數關系式;
(3)若嘉琪家五月和六月的月繳水費相差24元,求這兩月用水量差的最小值.
【答案】(1)3,5;(2)![]() ;(3)這兩月用水量差的最小值為4.8噸
;(3)這兩月用水量差的最小值為4.8噸
【解析】
(1)根據等量關系:“小明家1月份用水2016,交水費32元”;“53月份用水30噸,交水費65元”可列方程求解即可;
(2)根據(1)中所求的![]() 的值,可以得到收費標準,結合收費標準解答;
的值,可以得到收費標準,結合收費標準解答;
(3)設六月份用水t1噸,水費P1元,五月份用水t2噸,水費P2元,分情況討論即可求解.
(1)由題意得:![]() =
=![]() ,
,
15×3+(18﹣15)![]() =60,解得
=60,解得![]() =5,
=5,
故答案為:3;5;
(2)由(1)得:
![]() ;
;
(3)設六月份用水t1噸,水費P1元,五月份用水t2噸,水費P2元(t1>t2),
①若t1≤15,t2≤15,則t1﹣t2=24÷3=8;
②若t1>15,t2>15,則t1﹣t2=24÷5=4.8;
③若t2≤15<t1時,P1﹣P2=5t1﹣30﹣3t2=24,
∴![]() =
=![]() ,
,
∴t2=15時,t1﹣t2有最小值4.8.
綜上所述,這兩月用水量差的最小值為4.8噸.


科目:初中數學 來源: 題型:
【題目】如圖1,在直角坐標系中,直線l與x、y軸分別交于點A(4,0)、B(0,![]() )兩點,∠BAO的角平分線交y軸于點D. 點C為直線l上一點,以AC為直徑的⊙G經過點D,且與x軸交于另一點E.
)兩點,∠BAO的角平分線交y軸于點D. 點C為直線l上一點,以AC為直徑的⊙G經過點D,且與x軸交于另一點E.
(1)求證:y軸是⊙G的切線;
(2)求出⊙G的半徑r,并直接寫出點C的坐標;
(3)如圖2,若點F為⊙G上的一點,連接AF,且滿足∠FEA=45°,請求出EF的長?
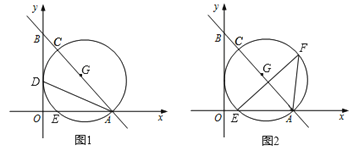
查看答案和解析>>
科目:初中數學 來源: 題型:
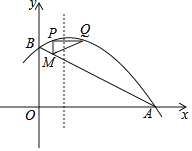
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+![]() x+2與x軸交于點A(4,0)與y軸交于點B.點M在線段AB上,其橫坐標為m,PM∥y軸,與拋物線交點為點P,PQ∥x軸,與拋物線交點為點Q
x+2與x軸交于點A(4,0)與y軸交于點B.點M在線段AB上,其橫坐標為m,PM∥y軸,與拋物線交點為點P,PQ∥x軸,與拋物線交點為點Q
(1)求a的值、并寫出此拋物線頂點的坐標;
(2)求m為何值時,△PMQ為等腰直角三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
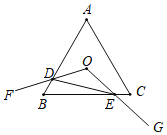
【題目】如圖,等邊△ABC的邊長為4,點O是△ABC的外心,∠FOG=120°.繞點O旋轉∠FOG,分別交線段AB、BC于D、E兩點.連接DE給出下列四個結論:①OD=OE;②S△ODE=S△BDE;③S四邊形ODBE=![]() ;④△BDE周長的最小值為6.上述結論中正確的個數是( )
;④△BDE周長的最小值為6.上述結論中正確的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了“創建文明城市,建設美麗臺州”,我市某社區將轄區內一塊不超過1000平方米的區域進行美化.經調查,美化面積為100平方米時,每平方米的費用為300元.每增加1平方米,每平方米的費用下降0.2元。設美化面積增加x平方米,美化所需總費用為y元.
(1)求y與x的函數關系式;
(2)當美化面積增加100平方米時,美化的總費用為多少元;
(3)當美化面積增加多少平方米時,美化所需費用最高?最高費用是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
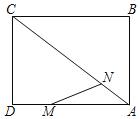
【題目】如圖,在矩形ABCD中,AB=6,AD=8,點M,N分別為AD,AC上的動點(不含端點),AN=DM,連結點M與矩形的一個頂點,以該線段為直徑作⊙O,當點N和矩形的另一個頂點也在⊙O上時,線段DM的長為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com