
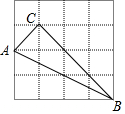
 如圖,在4×4的方格紙中,每個小方格的邊長都是1,△ABC的三個頂點分別在方格的格點上.
如圖,在4×4的方格紙中,每個小方格的邊長都是1,△ABC的三個頂點分別在方格的格點上.分析 (1)由矩形的面積減去三個直角三角形的面積即可;
(2)由勾股定理和勾股定理的逆定理證出△ABC是直角三角形,再由三角形面積關系即可得出結果.
解答 解:(1)△ABC的面積=3×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×3×3-$\frac{1}{2}$×1×1=3;
(2)∵AC2=12+12=2,BC2=32+32=18,AB2=22+42=20,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°,
∴AB邊上的高=$\frac{AC•BC}{AB}$=$\frac{\sqrt{2}×3\sqrt{2}}{2\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$.
點評 此題考查了勾股定理與勾股定理的逆定理.此題比較簡單,解題的關鍵是掌握勾股定理與勾股定理的逆定理的應用,掌握數形結合思想的應用.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
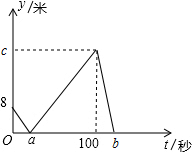 甲、乙兩人在直線跑道上同起點同終點同方向勻速跑步500米,先到終點的人原地休息.已知甲先出發2s,在跑步過程中,甲、乙兩人的距離y(m)與乙出發的時間t(s)之間的關系如圖所示,給出的下結論:①a=8,②c=92,③b=123,其中正確的是①②③.
甲、乙兩人在直線跑道上同起點同終點同方向勻速跑步500米,先到終點的人原地休息.已知甲先出發2s,在跑步過程中,甲、乙兩人的距離y(m)與乙出發的時間t(s)之間的關系如圖所示,給出的下結論:①a=8,②c=92,③b=123,其中正確的是①②③.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com