
【題目】拋物線y=ax+bx+4(a≠0)過點A(1, ﹣1),B(5, ﹣1),與y軸交于點C.
(1)求拋物線表達式;
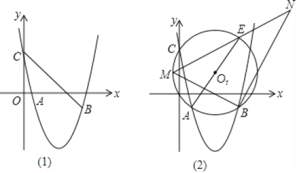
(2)如圖1,連接CB,以CB為邊作CBPQ,若點P在直線BC下方的拋物線上,Q為坐標平面內的一點,且CBPQ的面積為30,
①求點P坐標;
②過此二點的直線交y軸于F, 此直線上一動點G,當GB+![]() 最小時,求點G坐標.
最小時,求點G坐標.
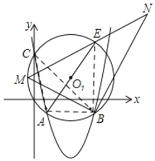
(3)如圖2,⊙O1過點A、B、C三點,AE為直徑,點M為 上的一動點(不與點A,E重合),∠MBN為直角,邊BN與ME的延長線交于N,求線段BN長度的最大值
【答案】(1)y=x﹣6x+4(2)①P(2, -4)或P(3, -5) ②G(0, -2)(3)![]()
【解析】
(1)把點A(1,-1),B(5,-1)代入拋物線y=ax2+bx+4解析式,即可得出拋物線的表達式;
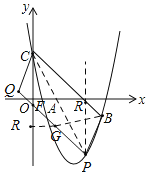
(2)①如圖,連接PC,過點P作y軸的平行線交直線BC于R,可求得直線BC的解析式為:y=-x+4,設點P(t,t2-6t+4),R(t,-t+4),因為CBPQ的面積為30,所以S△PBC=![]() ×(t+4t2+6t4)×5=15,解得t的值,即可得出點P的坐標;②當點P為(2,-4)時,求得直線QP的解析式為:y=-x-2,得F(0,-2),∠GOR=45°,因為GB+
×(t+4t2+6t4)×5=15,解得t的值,即可得出點P的坐標;②當點P為(2,-4)時,求得直線QP的解析式為:y=-x-2,得F(0,-2),∠GOR=45°,因為GB+![]()
GF=GB+GR,所以當G于F重合時,GB+GR最小,即可得出點G的坐標;當點P為(3,-5)時,同理可求;
(3)先用面積法求出sin∠ACB=![]() ,tan∠ACB=
,tan∠ACB=![]() ,在Rt△ABE中,求得圓的直徑,因為MB⊥NB,可得∠N=∠AEB=∠ACB,因為tanN=
,在Rt△ABE中,求得圓的直徑,因為MB⊥NB,可得∠N=∠AEB=∠ACB,因為tanN=![]() =
=![]() ,所以BN=
,所以BN=![]() MB,當MB為直徑時,BN的長度最大.
MB,當MB為直徑時,BN的長度最大.
(1) 解:(1)∵拋物線y=ax2+bx+4(a≠0)過點A(1,-1),B(5,-1),
∴![]() 解得
解得![]()
∴拋物線表達式為y=x﹣6x+4.
(2)①如圖,連接PC,過點P作y軸的平行線交直線BC于R,
設直線BC的解析式為y=kx+m,
∵B(5,-1),C(0,4),
∴![]() ,解得
,解得![]()
∴直線BC的解析式為:y=-x+4,
設點P(t,t2-6t+4),R(t,-t+4),
∵CBPQ的面積為30,
∴S△PBC=![]() ×(t+4t2+6t4)×5=15,
×(t+4t2+6t4)×5=15,
解得t=2或t=3,當t=2時,y=-4
當t=3時,y=-5,
∴點P坐標為(2,-4)或(3,-5);
②當點P為(2,-4)時,
∵直線BC解析式為:y=-x+4,QP∥BC,
設直線QP的解析式為:y=-x+n,
將點P代入,得-4=-2+n,n=-2,
∴直線QP的解析式為:y=-x-2,
∴F(0,-2),∠GOR=45°,
∴GB+![]() GF=GB+GR
GF=GB+GR
當G于F重合時,GB+GR最小,此時點G的坐標為(0,-2),
同理,當點P為(3,-5)時,直線QP的解析式為:y=-x-2,
同理可得點G的坐標為(0,-2),
(3) )∵A(1,-1),B(5,-1)C(0,4),
∴AC=![]() ,BC=5
,BC=5![]() ,
,
∵S△ABC=![]() AC×BCsin∠ACB=
AC×BCsin∠ACB=![]() AB×5,
AB×5,
∴sin∠ACB=![]() ,tan∠ACB=
,tan∠ACB=![]() ,
,
∵AE為直徑,AB=4,
∴∠ABE=90°,
∵sin∠AEB=sin∠ACB=![]() =
=![]() ,
,
∴AE=2![]() ,
,
∵MB⊥NB,∠NMB=∠EAB,
∴∠N=∠AEB=∠ACB,
∴tanN=![]() =
=![]() ,
,
∴BN=![]() MB,
MB,
當MB為直徑時,BN的長度最大,為3![]() .
.


科目:初中數學 來源: 題型:
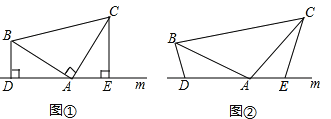
【題目】(1)如圖①,已知:在△ABC中,∠BAC=90°,AB=AC,直線m經過點A,BD⊥直線m, CE⊥直線m,垂足分別為點D、E.證明:DE=BD+CE.
(2)如圖②,將(1)中的條件改為:在△ABC中,AB=AC,D、A、E三點都在直線m上,并且有∠BDA=∠AEC=∠BAC=α,其中α為任意鈍角.請問結論DE=BD+CE是否成立?如成立,請你給出證明;若不成立,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為配合“一帶一路”國家倡議,某鐵路貨運集裝箱物流園區正式啟動了2期擴建工程一項地基基礎加固處理工程由2、8兩個工程公司承擔建設,己知2工程公司單獨建設完成此項工程需要180天![]() 工程公司單獨施工天后,
工程公司單獨施工天后,![]() 工程公司參與合作,兩工程公司又共同施工
工程公司參與合作,兩工程公司又共同施工![]() 天后完成了此項工程.
天后完成了此項工程.
(1)求![]() 工程公司單獨建設完成此項工程需要多少天?
工程公司單獨建設完成此項工程需要多少天?
(2)由于受工程建設工期的限制,物流園區管委會決定將此項工程劃包成兩部分,要求兩工程公司同時開工,![]() 工程公司建設其中一部分用了
工程公司建設其中一部分用了![]() 天完成,
天完成,![]() 工程公司建設另一部分用了
工程公司建設另一部分用了![]() 天完成,其中
天完成,其中![]() ,
,![]() 均為正整數,且
均為正整數,且![]() ,
,![]() ,求
,求![]() 、
、![]() 兩個工程公司各施工建設了多少天?
兩個工程公司各施工建設了多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年是我市全面推進中小學校“社會主義核心價值觀”教育年.某校對全校學生進行了中期檢測評價,檢測結果分為![]() (優秀)、
(優秀)、![]() (良好)、
(良好)、![]() (合格)、
(合格)、![]() (不合格)四個等級.并隨機抽取若干名學生的檢測結果作為樣本進行數據處理,制作了如下所示不完整的統計表(圖1)和統計圖(圖2).
(不合格)四個等級.并隨機抽取若干名學生的檢測結果作為樣本進行數據處理,制作了如下所示不完整的統計表(圖1)和統計圖(圖2).
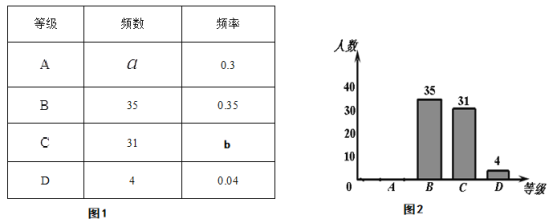
請根據圖1、圖2提供的信息,解答下列問題:
(1)本次隨機抽取的樣本容量為
(2)![]() ,
,![]() .
.
(3)請在圖2中補全條形統計圖.
(4)若該校共有學生800人,據此估算,該校學生在本次檢測中達到“![]() (優秀)”等級的學生人數為 人.
(優秀)”等級的學生人數為 人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠BAC=45°,將△ABC繞點A逆時針方向旋轉得△AEF,其中,E,F是點B,C旋轉后的對應點,BE,CF相交于點D.若四邊形ABDF為菱形,則∠CAE的大小是( )
![]()
A. 45°B. 60°C. 75°D. 90°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市實施產業精準扶貧,幫助貧困戶承包荒山種植某品種蜜柚.已知該蜜柚的成本價為6元/千克,到了收獲季節投入市場銷售時,調查市場行情后,發現該蜜柚不會虧本,且每天的銷售量y(千克)與銷售單價x(元)之間的函數關系如圖所示.
(1)求y與x的函數關系式,并寫出x的取值范圍;
(2)當該品種蜜柚定價為多少時,每天銷售獲得的利潤最大?最大利潤是多少?
(3)某村農戶今年共采摘蜜柚12000千克,若該品種蜜柚的保質期為50天,按照(2)的銷售方式,能否在保質期內全部銷售完這批蜜柚?若能,請說明理由;若不能,應定銷售價為多少元時,既能銷售完又能獲得最大利潤?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的方程(x﹣3)(x﹣5)=m(m>0)有兩個實數根α,β(α<β),則下列選項正確的是( )
A. 3<α<β<5 B. 3<α<5<β C. α<2<β<5 D. α<3且β>5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將△ABC繞點C順時針旋轉90°得到△EDC.若點A,D,E在同一條直線上,∠ACB=20°,則∠ADC的度數是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com