
【題目】已知拋物線![]() 與x軸交于A.B兩點,與y軸交于C點,拋物線的頂點為D點,點A的坐標為(﹣1,0).
與x軸交于A.B兩點,與y軸交于C點,拋物線的頂點為D點,點A的坐標為(﹣1,0).
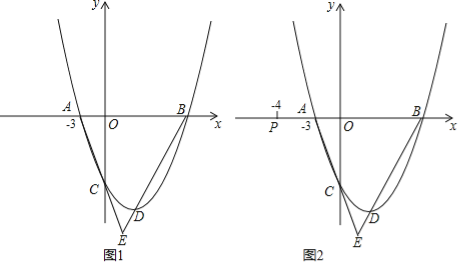
(1)求D點的坐標;
(2)如圖1,連接AC,BD并延長交于點E,求∠E的度數(shù);
(3)如圖2,已知點P(﹣4,0),點Q在x軸下方的拋物線上,直線PQ交線段AC于點M,當∠PMA=∠E時,求點Q的坐標.
【答案】(1)頂點D的坐標為(1,﹣4)。
(2)∠E=45°
(3)點Q的坐標為(2,﹣3)或(![]() ,
,![]() )。
)。
【解析】
(1)將點A的坐標代入到拋物線的解析式求得c值,然后配方后即可確定頂點D的坐標。
(2)連接CD、CB,過點D作DF⊥y軸于點F,首先求得點C的坐標,然后證得△DCB∽△AOC得到∠CBD=∠OCA,根據(jù)∠ACB=∠CBD+∠E=∠OCA+∠OCB,得到∠E=∠OCB=45°。
(3)設(shè)直線PQ交y軸于N點,交BD于H點,作DG⊥x軸于G點,增大△DGB∽△PON后利用相似三角形的性質(zhì)求得ON的長,從而求得點N的坐標,進而求得直線PQ的解析式,設(shè)Q(m,n),根據(jù)點Q在直線PQ和拋物線![]() 上,得到
上,得到![]() ,求得m、n的值后即可求得點Q的坐標。
,求得m、n的值后即可求得點Q的坐標。
解:(1)把x=﹣1,y=0代入![]() 得:1+2+c=0,∴c=﹣3。
得:1+2+c=0,∴c=﹣3。
∴![]() 。
。
∴頂點D的坐標為(1,﹣4)。
(2)如圖1,連接CD、CB,過點D作DF⊥y軸于點F,
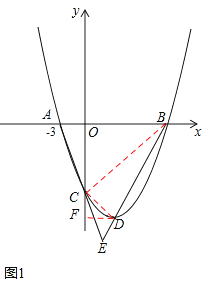
由![]() 解得x=﹣1或x=3,∴B(3,0)。
解得x=﹣1或x=3,∴B(3,0)。
當x=0時,![]() ,∴C(0,﹣3)。
,∴C(0,﹣3)。
∴OB=OC=3。
∵∠BOC=90°,∴∠OCB=45°,BC=![]() 。
。
又∵DF=CF=1,∠CFD=90°,
∴∠FCD=45°,CD=![]() 。
。
∴∠BCD=180°﹣∠OCB﹣∠FCD=90°
∴∠BCD=∠COA。
又∵![]() ,∴△DCB∽△AOC。
,∴△DCB∽△AOC。
又∵∠ACB=∠CBD+∠E=∠OCA+∠OCB,∴∠E=∠OCB=45°。
(3)如圖2,設(shè)直線PQ交y軸于N點,交BD于H點,作DG⊥x軸于G點,
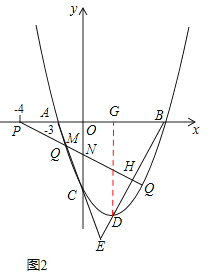
∵∠PMA=45°,∴∠EMH=45°。∴∠MHE=90°。
∴∠PHB=90°。∴∠DBG+∠OPN=90°。
又∵∠ONP+∠OPN=90°,∴∠DBG=∠ONP。
又∵∠DGB=∠PON=90°,∴△DGB=∠PON=90°。
∴△DGB∽△PON。
∴![]() ,即
,即![]() ,解得ON=2。
,解得ON=2。
∴N(0,﹣2)。
設(shè)直線PQ的解析式為y=kx+b,
則![]() ,解得:
,解得: 。
。
∴直線PQ的解析式為![]() 。
。
設(shè)Q(m,n)且n<0,∴![]() 。
。
又∵Q(m,n)在![]() 上,∴
上,∴![]() 。
。
∴![]() ,解得:m=2或m=
,解得:m=2或m=![]() 。
。
∴n=﹣3或n=![]() 。
。
∴點Q的坐標為(2,﹣3)或(![]() ,
,![]() )。
)。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:初中數(shù)學(xué) 來源: 題型:
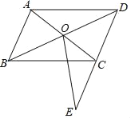
【題目】如圖,在ABCD中,對角線AC、BD相交于點O,在DC的延長線上取一點E,連接OE交BC于點F,已知AB=6,BC=8,CE=2
(1)求CF的長.
(2)設(shè)△COF的面積為S1,△COD的面積為S2,直接寫出S1:S2的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直線![]() ,連接
,連接![]() ,
,![]() 為一動點.
為一動點.
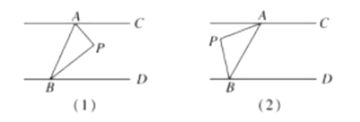
(1)當動點![]() 落在如圖
落在如圖![]() 所示的位置時,連接
所示的位置時,連接![]() ,求證:
,求證:![]() ;
;
(2)當動點![]() 落在如圖
落在如圖![]() 所示的位置時,連接
所示的位置時,連接![]() ,則
,則![]() 之間的關(guān)系如何,你得出的結(jié)論是 .(只寫結(jié)果,不用寫證明)
之間的關(guān)系如何,你得出的結(jié)論是 .(只寫結(jié)果,不用寫證明)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標系中,A,B兩點的坐標分別是(0,4),(0,﹣4),點C是x軸上一個動點,過點B作直線BH⊥AC于點H,過點C作CD∥y軸,交BH于點D,點C在x軸上運動的過程中,點D不可能經(jīng)過的點是( )
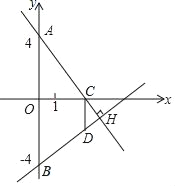
A. (2,﹣3) B. (1,﹣3) C. (4,0) D. (0,﹣4)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形網(wǎng)格中的每個小正方形的邊長都是1,每個小正方形的頂點叫做格點.△ABC的三個頂點A,B,C都在格點上.將△ABC繞點A按順時針方向旋轉(zhuǎn)90°得到△AB′C′.
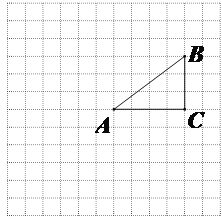
(1)在正方形網(wǎng)格中,畫出△AB′C′;
(2)計算線段AB在變換到AB′的過程中掃過的區(qū)域的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】二次函數(shù)y=ax2+bx+c,自變量x與函數(shù)y的對應(yīng)值如表:
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
下列說法正確的是( )
A. 拋物線的開口向下
B. 當x>﹣![]() 時,y隨x的增大而增大
時,y隨x的增大而增大
C. 二次函數(shù)的最小值是﹣2
D. 拋物線的對稱軸是x=1
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(本小題6分)為了參加中考體育測試,甲,乙,丙三位同學(xué)進行足球傳球訓(xùn)練。球從一個人
腳下隨機傳到另一個人腳下,且每位傳球人傳球給其余兩人的機會是均等的,由甲開始傳球,共傳三次。
(1)求請用樹狀圖列舉出三次傳球的所有可能情況;
(2)傳球三次后,球回到甲腳下的概率;
(3)三次傳球后,球回到甲腳下的概率大還是傳到乙腳下的概率大?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】2018年10月,吉州區(qū)井岡蜜柚節(jié)迎來了四方游客,游客李先生選購了井岡蜜柚和井岡板栗各一箱需要200元.他還準備給4位朋友每人送同樣的井岡蜜柚一箱,6位同事每人送同樣的井岡板栗一箱,就還需要1040元.
(1)求每箱井岡蜜柚和每箱井岡板栗各需要多少元?
(2)李先生到收銀臺才得知井岡蜜柚節(jié)期間,井岡蜜柚可以享受6折優(yōu)惠,井岡板栗可以享受8折優(yōu)惠,此時李先生比預(yù)計的付款少付了多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
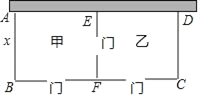
【題目】林場要建一個果園(矩形ABCD),果園的一面靠墻(墻最大可用長度為30米),另三邊用木欄圍成,中間EF也用木欄隔開,分為甲、乙兩個場地,并在如圖所示的三處各留1米寬的門(不用木欄),木欄總長57米.設(shè)果園(矩形ABCD)的寬AB為x米,矩形ABCD的面積為S平方米.
(1)求S關(guān)于x的函數(shù)表達式,并寫出自變量x的取值范圍.
(2)求果園能達到的最大面積S及相應(yīng)x的值.
(3)若木欄BF比CF多10米,其余條件不變,甲場地種植葡萄,一季平均每平方米收益40元;乙場地種植益莓,一季平均每平方米收益160元.問該果園一季能達到的最大收益W為多少元?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com