
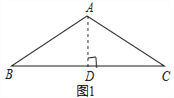
【題目】問題背景:如圖1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于點D,則D為BC的中點,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() ;
;
遷移應用:如圖2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三點在同一條直線上,連接BD.
(1)求證:△ADB≌△AEC;
(2)若AD=2,BD=3,請計算線段CD的長;
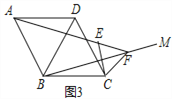
拓展延伸:如圖3,在菱形ABCD中,∠ABC=120°,在∠ABC內作射線BM,作點C關于BM的對稱點E,連接AE并延長交BM于點F,連接CE,CF.
(3)證明:△CEF是等邊三角形;
(4)若AE=4,CE=1,求BF的長.

【答案】(1)見解析;(2)CD =![]() ;(3)見解析;(4)
;(3)見解析;(4)![]()
【解析】試題分析:遷移應用:(1)如圖2中,只要證明∠DAB=∠CAE,即可根據SAS解決問題;
(2)結論:CD=![]() AD+BD.由△DAB≌△EAC,可知BD=CE,在Rt△ADH中,DH=ADcos30°=
AD+BD.由△DAB≌△EAC,可知BD=CE,在Rt△ADH中,DH=ADcos30°=![]() AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD=
AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD=![]() AD+BD,即可解決問題;
AD+BD,即可解決問題;
拓展延伸:(3)如圖3中,作BH⊥AE于H,連接BE.由BC=BE=BD=BA,FE=FC,推出A、D、E、C四點共圓,推出∠ADC=∠AEC=120°,推出∠FEC=60°,推出△EFC是等邊三角形;
(4)由AE=4,EC=EF=1,推出AH=HE=2,FH=3,在Rt△BHF中,由∠BFH=30°,可得![]() =cos30°,由此即可解決問題.
=cos30°,由此即可解決問題.
試題解析:
遷移應用:(1)證明:如圖2,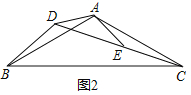
∵∠BAC=∠DAE=120°,
∴∠DAB=∠CAE,
在△DAE和△EAC中,
DA=EA,∠DAB=∠EAC,AB=AC,
∴△DAB≌△EAC,
(2)結論:CD=![]() AD+BD.
AD+BD.
理由:如圖2-1中,作AH⊥CD于H.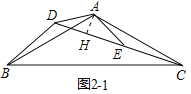
∵△DAB≌△EAC,
∴BD=CE,
在Rt△ADH中,DH=ADcos30°=![]() AD,
AD,
∵AD=AE,AH⊥DE,
∴DH=HE,
∵CD=DE+EC=2DH+BD=![]() AD+BD=
AD+BD=![]() .
.
拓展延伸:(3)如圖3中,作BH⊥AE于H,連接BE.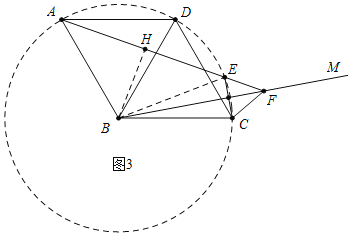
∵四邊形ABCD是菱形,∠ABC=120°,
∴△ABD,△BDC是等邊三角形,
∴BA=BD=BC,
∵E、C關于BM對稱,
∴BC=BE=BD=BA,FE=FC,
∴A、D、E、C四點共圓,
∴∠ADC=∠AEC=120°,
∴∠FEC=60°,
∴△EFC是等邊三角形,
(4)∵AE=4,EC=EF=1,
∴AH=HE=2,FH=3,
在Rt△BHF中,∵∠BFH=30°,
∴![]() =cos30°,
=cos30°,
∴BF=![]() .
.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】對于任意四個有理數a,b,c,d,可以組成兩個有理數對(a,b)與(c,d).我們規定:
(a,b)★(c,d)=bc-ad.
例如:(1,2)★(3,4)=2×3-1×4=2.
根據上述規定解決下列問題:
(1)有理數對(2,-3)★(3,-2)=_______;
(2)若有理數對(-3,2x-1)★(1,x+1)=7,則x=_______;
(3)當滿足等式(-3,2x-1)★(k,x+k)=5+2k的x是整數時,求整數k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=30°,將△ABC繞點C逆時針旋轉得到△DEC,點A的對應點D恰好落在線段CB的延長線上,連接AD,若∠ADE=90°,則∠BAD=_________
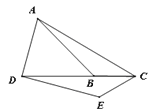
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校組織七、八年級全體同學參觀八路軍太行紀念館(位于山西省長治市武鄉縣城).七年級租用45座大巴車![]() 輛,55座大巴車
輛,55座大巴車![]() 輛;八年級租用30座中巴車
輛;八年級租用30座中巴車![]() 輛,55座大巴車
輛,55座大巴車![]() 輛.當每輛車恰好坐滿時:
輛.當每輛車恰好坐滿時:

(1)用含有![]() ,
,![]() 的代數式分別表示七、八年級各有學生數.
的代數式分別表示七、八年級各有學生數.
(2)用含有![]() ,
,![]() 的代數式表示七、八年級共有多少學生?
的代數式表示七、八年級共有多少學生?
(3)當![]() ,
,![]() 時,該學校七、八年級共有多少學生?
時,該學校七、八年級共有多少學生?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的袋子中裝有紅、白兩種顏色的小球,這些球除顏色外完全相同,其中紅球有![]() 個,若從中隨機摸出一個球,這個球是白球的概率為
個,若從中隨機摸出一個球,這個球是白球的概率為![]() .
.
(![]() )請直接寫出袋子中白球的個數.
)請直接寫出袋子中白球的個數.
(![]() )隨機摸出一個球后,放回并攪勻,再隨機摸出一個球,求兩次都摸到相同顏色的小球的概率.(請結合樹狀圖或列表解答)
)隨機摸出一個球后,放回并攪勻,再隨機摸出一個球,求兩次都摸到相同顏色的小球的概率.(請結合樹狀圖或列表解答)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為半圓O的直徑,以AO為直徑作半圓M,C為OB的中點,D在半圓M上,且CD⊥MD,延長AD交半圓O于點E,且AB=4,則圓中陰影部分的面積為_____________.
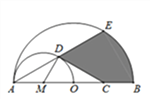
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下面三行數:
①-3,9,-27,81,-243,729,…;
②0,12,-24,84,-240,732,…;
③-1,3,-9,27,-81,243,….
(1)第①行數有什么規律?
(2)第②行數與第①行數有什么關系?
(3)第③行數與第①行數有什么關系?
(4)取每行數的第10個數,計算這三個數的和.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 與x軸相交于A、B兩點,與y軸相交于點C(0,4),若已知A點的坐標為A(﹣2,0).
與x軸相交于A、B兩點,與y軸相交于點C(0,4),若已知A點的坐標為A(﹣2,0).
(1)求拋物線的解析式;
(2)求△ABC的外接圓圓心坐標;
(3)在拋物線的對稱軸上是否存在點Q,使△ACQ為等腰三角形?若存在,求出符合條件的Q點坐標,若不存在,請說明理由.
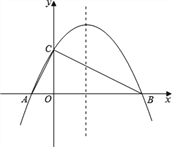
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與探究
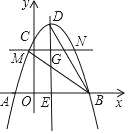
如圖,拋物線y=﹣![]() x2+2x+6與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,其對稱軸與拋物線交于點D.與x軸交于點E.
x2+2x+6與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,其對稱軸與拋物線交于點D.與x軸交于點E.
(1)求點A,B,D的坐標;
(2)點G為拋物線對稱軸上的一個動點,從點D出發,沿直線DE以每秒2個單位長度的速度運動,過點C作x軸的平行線交拋物線于M,N兩點(點M在點N的左邊).
設點G的運動時間為ts.
①當t為何值時,以點M,N,B,E為頂點的四邊形是平行四邊形;
②連接BM,在點G運動的過程中,是否存在點M.使得∠MBD=∠EDB,若存在,求出點M的坐標;若不存在,請說明理由;
(3)點Q為坐標平面內一點,以線段MN為對角線作萎形MENQ,當菱形MENQ為正方形時,請直接寫出t的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com