若半徑為5和4的兩圓相交于A、B,且AB=6,則它們的圓心距d等于 .
【答案】
分析:有兩種情況:兩圓相外交,連接O
1O
2交AB與C點,連接O
1A、O
2A,再分別求出O
2C、O
1C的值,即可求得圓心距d;
兩圓相內交時,連接O
1O
2并延長交AB與C點,連接O
1A、O
2A,再求出O
2C、O
1C的值,即可求得圓心距d.
解答:解:兩圓相交有兩種情況:
兩圓相外交,連接O
1O
2交AB與C點,連接O
1A、O
2A,如下圖所示,

由題意知,AB=6,O
1A=4,O
2B=5;
∵AB為兩圓交點,
∴O
1O
2垂直平分AB,
∴AC=3;
在Rt△O
1AC和Rt△O
2AC中,由勾股定理可得,
O
2C=4,O
1C=
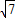
,
所以,圓心距d=O
2C+O
1C=4+

;
兩圓相內交時,連接O
1O
2并延長交AB與C點,連接O
1A、O
2A,如下圖所示,
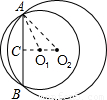
由題意可知,AB=6,O
1A=4,O
2A=5;
∵AB為兩圓交點,
∴O
2C垂直平分AB,
∴AC=3;
在Rt△O
1AC和Rt△O
2AC中,由勾股定理可得,
O
2C=4,O
1C=

,
所以,圓心距d=O
2C-O
1C=4-
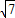
;
綜上所述,圓心距d為4+
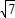
或4-
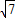
.
故此題應該填4+
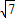
或4-
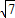
.
點評:本題考查了相交兩圓的性質.


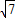 ,
, ;
;
 ,
,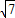 ;
;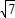 或4-
或4-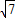 .
.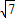 或4-
或4-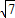 .
.

 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案