
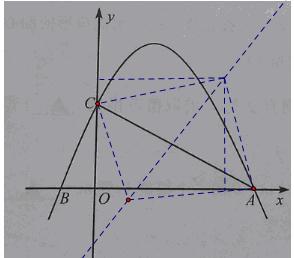
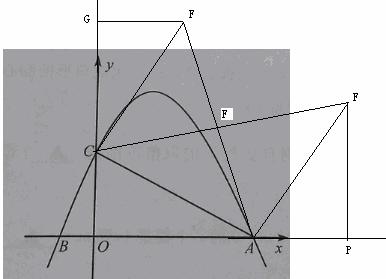
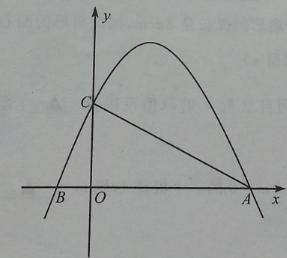
在平面直角坐標系 中,二次函數
中,二次函數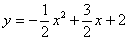 的圖像與
的圖像與 軸交于點A,B(點B在點A的左側),與
軸交于點A,B(點B在點A的左側),與 軸交于點C.過動點H(0,
軸交于點C.過動點H(0,  )作平行于
)作平行于 軸的直線,直線與二次函數
軸的直線,直線與二次函數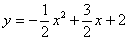 的圖像相交于點D,E.
的圖像相交于點D,E.
(1)寫出點A,點B的坐標;
(2)若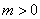 ,以DE為直徑作⊙Q,當⊙Q與
,以DE為直徑作⊙Q,當⊙Q與 軸相切時,求
軸相切時,求 的值;
的值;
(3)直線上是否存在一點F,使得△ACF是等腰直角三角形?若存在,求 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
解:(1)當 =0時,有
=0時,有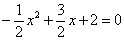 ,解之得:
,解之得: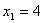 ,
,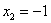 ,∴A、B兩點的坐標分別為(4,0)和(-1,0).
,∴A、B兩點的坐標分別為(4,0)和(-1,0).
(2)∵⊙Q與 軸相切,且與
軸相切,且與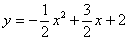 交于D、E兩點,
交于D、E兩點,
∴圓心O位于直線與拋物線對稱軸的交點處,且⊙Q的半徑為H點的縱坐標 (
(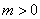 )
)
∵拋物線的對稱軸為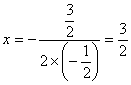 ,
,
∴D、E兩點的坐標分別為:(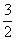 -
- ,
, ),(
),(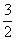 +
+ ,
, )且均在二次函數
)且均在二次函數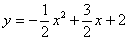 的圖像上,
的圖像上,
∵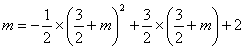 ,解得
,解得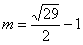 或
或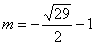 (不合題意,舍去)
(不合題意,舍去)
(3)存在.
①當∠ACF=90°,AC=FC時,過點F作FG⊥ 軸于G,∴∠AOC=∠CGF=90°,
軸于G,∴∠AOC=∠CGF=90°,
∵∠ACO+∠FCG=90°,∠GFC+∠FCG=90°,∴∠ACO=∠CFG,∴△ACO≌△∠CFG,∴CG=AO=4,
∵CO=2,∴ =OG=2+4=6;
=OG=2+4=6;
②當∠CAF=90°,AC=AF時,過點F作FP⊥ 軸于P,∴∠AOC=∠APF=90°,
軸于P,∴∠AOC=∠APF=90°,
∵∠ACO+∠OAC=90°,∠FAP+∠OAC=90°,∴∠ACO=∠FAP,∴△ACO≌△∠FAP,∴FP =AO=4,
∴ =FP =4;
=FP =4;
③當∠AFC=90°,FA=FC時,則F點一定在AC的中垂線上,此時 =3或
=3或 =1
=1


科目:初中數學 來源: 題型:
如圖1,矩形OABC頂點B的坐標為(8,3),定點D的坐標為(12,0),動點P從點O出發,以每秒2個單位長度的速度沿x軸的正方向勻速運動,動點Q從點D出發,以每秒1個單位長度的速度沿x軸的負方向勻速運動,PQ兩點同時運動,相遇時停止.在運動過程中,以PQ為斜邊在x軸上方作等腰直角三角形PQR.設運動時間為t秒.
(1)當t= 時,△PQR的邊QR經過點B;
(2)設△PQR和矩形OABC重疊部分的面積為S,求S關于t的函數關系式;
(3)如圖2,過定點E(5,0)作EF⊥BC,垂足為F,當△PQR的頂點R落在矩形OABC的內部時,過點R作x軸、y軸的平行線,分別交EF、BC于點M、N,若∠MAN=45°,求t的值.
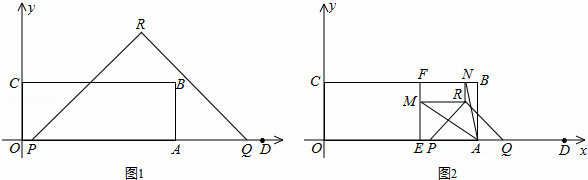
查看答案和解析>>
科目:初中數學 來源: 題型:
下列整數中,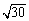 與最接近的是········································································ ( )
與最接近的是········································································ ( )
A.4 B.5 C.6 D.7
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com