
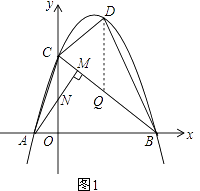
【題目】如圖1,在平面直角坐標系中,直線l與x軸、y軸分別交于點B(4,0)、C(0,3),點A為x軸負半軸上一點,AM⊥BC于點M交y軸于點N,滿足4CN=5ON.已知拋物線y=ax2+bx+c經過點A、B、C.
(1)求拋物線的函數關系式;
(2)連接AC,點D在線段BC上方的拋物線上,連接DC、DB,若△BCD和△ABC面積滿足S△BCD= ![]() S△ABC , 求點D的坐標;
S△ABC , 求點D的坐標;
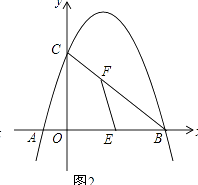
(3)如圖2,E為OB中點,設F為線段BC上一點(不含端點),連接EF.一動點P從E出發,沿線段EF以每秒1個單位的速度運動到F,再沿著線段FC以每秒 ![]() 個單位的速度運動到C后停止.若點P在整個運動過程中用時最少,請直接寫出最少時間和此時點F的坐標.
個單位的速度運動到C后停止.若點P在整個運動過程中用時最少,請直接寫出最少時間和此時點F的坐標.
【答案】
(1)
解:∵C(0,3),
∴OC=3,
∵4CN=5ON,
∴ON= ![]() ,
,
∵∠OAN=∠NCM,
∴△AON∽△COB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得OA=1,
,解得OA=1,
∴A(﹣1,0),
設拋物線解析式為y=a(x+1)(x﹣4),
把C(0,3)代入得a1(﹣4)=3,解得a=﹣ ![]() ,
,
∴拋物線解析式為y=﹣ ![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣ ![]() x2+
x2+ ![]() x+3;
x+3;
(2)
解:設直線BC的解析式為y=mx+n,
把C(0,3),B(4,0)代入得 ![]() ,解得
,解得  ,
,
∴直線BC的解析式為y=﹣ ![]() x+3,
x+3,
作PQ∥y軸交BC于Q,如圖1,
設P(x,﹣ ![]() x2+
x2+ ![]() x+3),則Q(x,﹣
x+3),則Q(x,﹣ ![]() x+3),
x+3),
DQ=﹣ ![]() x2+
x2+ ![]() x+3﹣(﹣
x+3﹣(﹣ ![]() x+3)=﹣
x+3)=﹣ ![]() x2+3x,
x2+3x,
∴S△BCD=S△CDQ+S△BDQ= ![]() 4(﹣
4(﹣ ![]() x2+3x)=﹣
x2+3x)=﹣ ![]() x2+6x,
x2+6x,
∵S△BCD= ![]() S△ABC,
S△ABC,
∴﹣ ![]() x2+6x=
x2+6x= ![]() ×
× ![]() ×(4+1)×3,
×(4+1)×3,
整理得x2﹣4x+3=0,解得x1=1,x2=3,
∴D點坐標為(1, ![]() )或(3,3);
)或(3,3);
(3)
解:設F(m,﹣ ![]() x+3),則EF=
x+3),則EF= ![]() =
= ![]() ,CF=
,CF= ![]() ,
,
點P在整個運動過程中所用時間t=EF+ ![]() =EF+
=EF+ ![]() CF≥2
CF≥2 ![]() ,當EF=
,當EF= ![]() CF時,取等號,此時t最小,
CF時,取等號,此時t最小,
即 ![]() x2﹣
x2﹣ ![]() x+13=(
x+13=( ![]()
![]() x)2,
x)2,
整理得2x2﹣17x+26,解得x1=2,x2= ![]() (舍去),
(舍去),
∴點P在整個運動過程中所用的最少時間2× ![]() ×2=3秒,此時點F的坐標為(2,
×2=3秒,此時點F的坐標為(2, ![]() ).
).
【解析】(1)先利用OC=3和4CN=5ON計算出ON= ![]() ,再證明△AON∽△COB,利用相似比計算出OA=1,得到A(﹣1,0),然后利用交點式可求出拋物線解析式為y=﹣
,再證明△AON∽△COB,利用相似比計算出OA=1,得到A(﹣1,0),然后利用交點式可求出拋物線解析式為y=﹣ ![]() x2+
x2+ ![]() x+3;(2)先利用待定系數法求出直線BC的解析式為y=﹣
x+3;(2)先利用待定系數法求出直線BC的解析式為y=﹣ ![]() x+3,作PQ∥y軸交BC于Q,如圖1,設P(x,﹣
x+3,作PQ∥y軸交BC于Q,如圖1,設P(x,﹣ ![]() x2+
x2+ ![]() x+3),則Q(x,﹣
x+3),則Q(x,﹣ ![]() x+3),再計算出DQ=﹣
x+3),再計算出DQ=﹣ ![]() x2+3x,根據三角形面積公式得S△BCD=S△CDQ+S△BDQ=﹣
x2+3x,根據三角形面積公式得S△BCD=S△CDQ+S△BDQ=﹣ ![]() x2+6x,然后根據S△BCD=
x2+6x,然后根據S△BCD= ![]() S△ABC得到﹣
S△ABC得到﹣ ![]() x2+6x=
x2+6x= ![]() ×
× ![]() ×(4+1)×3,然后解方程求出x即可得到D點坐標;(3)設F(m,﹣
×(4+1)×3,然后解方程求出x即可得到D點坐標;(3)設F(m,﹣ ![]() x+3)利用兩點間的距離公式得到EF=
x+3)利用兩點間的距離公式得到EF= ![]() ,CF=
,CF= ![]() x,則點P在整個運動過程中所用時間t=EF+
x,則點P在整個運動過程中所用時間t=EF+ ![]() =EF+
=EF+ ![]() CF,根據不等式公式得到EF+
CF,根據不等式公式得到EF+ ![]() CF≥2
CF≥2 ![]() ,當EF=
,當EF= ![]() CF時,取等號,此時t最小,解方程
CF時,取等號,此時t最小,解方程 ![]() x2﹣
x2﹣ ![]() x+13=(
x+13=( ![]()
![]() x)2得x1=2,x2=
x)2得x1=2,x2= ![]() (舍去),于是得到點P在整個運動過程中所用的最少時間2×
(舍去),于是得到點P在整個運動過程中所用的最少時間2× ![]() ×2=3秒,此時點F的坐標為(2,
×2=3秒,此時點F的坐標為(2, ![]() ).
).


 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:初中數學 來源: 題型:
【題目】對于二次函數y=x2﹣3x+2和一次函數y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)稱為這兩個函數的“再生二次函數”,其中t是不為零的實數,其圖像記作拋物線E,現有點A(2,0)和拋物線E上的點B(﹣1,n),請完成下列任務;
(1)【嘗試】①當t=2時,拋物線y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)的頂點坐標為
(2)②判斷點A是否在拋物線E上;
(3)③求n的值.
(4)【發現】通過(2)和(3)的演算可知,對于t取任何不為零的實數,拋物線E總過定點,坐標為 .
(5)【應用】
①二次函數y=﹣3x2+5x+2是二次函數y=x2﹣3x+3和一次函數y=﹣2x+4的一個“再生二次函數”嗎?如果是,求出t的值;如果不是,說明理由;
②以AB為邊作矩形ABCD,使得其中一個頂點落在y軸上;若拋物線E經過A,B,C,D其中的三點,求出所有符合條件的t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初三年級教師對試卷講評課中學生參與的深度與廣度進行評價調查,其評價項目為主動質疑、獨立思考、專注聽講、講解題目四項.評價組隨機抽取了若干名初中學生的參與情況,繪制成如圖所示的頻數分布直方圖和扇形統計圖(均不完整),請根據圖中所給信息解答下列問題: 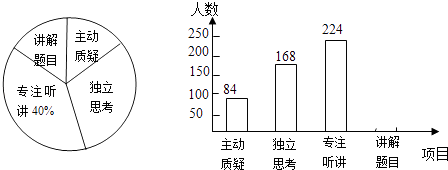
(1)在這次評價中,一共抽查了名學生;
(2)在扇形統計圖中,項目“主動質疑”所在的扇形的圓心角的度數為度;
(3)請將頻數分布直方圖補充完整;
(4)如果全市有6000名初三學生,那么在試卷評講課中,“獨立思考”的初三學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,E是AD邊上的中點,連接BE,并延長BE交CD的延長線于點F. 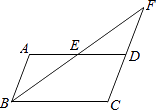
(1)證明:FD=AB;
(2)當ABCD的面積為8時,求△FED的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,點E在邊DC上,DE:EC=3:1,連接AE交BD于點F,則△DEF的面積與△BAF的面積之比為( ) 
A.3:4
B.9:16
C.4:9
D.1:3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=ax+b(a≠0)的圖形與反比例函數y= ![]() (k≠0)的圖象交于第二、四象限內的A、B兩點,與y軸交于C點,過點A作AH⊥y軸,垂足為H,OH=3,tan∠AOH=
(k≠0)的圖象交于第二、四象限內的A、B兩點,與y軸交于C點,過點A作AH⊥y軸,垂足為H,OH=3,tan∠AOH= ![]() ,點B的坐標為(m,﹣2).
,點B的坐標為(m,﹣2). 
(1)求該反比例函數和一次函數的解析式.
(2)求△AOC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】課本中有一個例題:
有一個窗戶形狀如圖1,上部是一個半圓,下部是一個矩形,如果制作窗框的材料總長為6m,如何設計這個窗戶,使透光面積最大?
這個例題的答案是:當窗戶半圓的半徑約為0.35m時,透光面積最大值約為1.05m2 .
我們如果改變這個窗戶的形狀,上部改為由兩個正方形組成的矩形,如圖2,材料總長仍為6m,利用圖3,解答下列問題:
(1)若AB為1m,求此時窗戶的透光面積?
(2)與課本中的例題比較,改變窗戶形狀后,窗戶透光面積的最大值有沒有變大?請通過計算說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次函數y=ax+b和反比例函數y= ![]() 在同一平面直角坐標系中的圖象如圖所示,則二次函數y=ax2+bx+c的圖象大致為( )
在同一平面直角坐標系中的圖象如圖所示,則二次函數y=ax2+bx+c的圖象大致為( ) 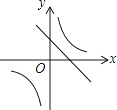
A.
B.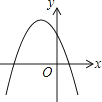
C.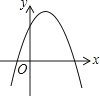
D.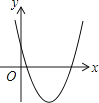
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com