
【題目】題目:為了美化環(huán)境,某地政府計劃對轄區(qū)內(nèi)![]() 的土地進(jìn)行綠化.為了盡快完成任務(wù),實際平均每月的綠化面積是原計劃的1.5倍,結(jié)果提前2個月完成任務(wù).求原計劃平均每月的綠化面積.
的土地進(jìn)行綠化.為了盡快完成任務(wù),實際平均每月的綠化面積是原計劃的1.5倍,結(jié)果提前2個月完成任務(wù).求原計劃平均每月的綠化面積.
甲同學(xué)所列的方程為![]()
乙同學(xué)所列的方程為![]()
(1)甲同學(xué)所列的方程中![]() 表示 .乙同學(xué)所列的方程中
表示 .乙同學(xué)所列的方程中![]() 表示 .
表示 .
(2)任選甲、乙兩同學(xué)的其中一個方法解答這個題目.
【答案】(1)原計劃平均每月的綠化面積,實際完成這項工程需要的月數(shù);(2)10,解答見解析
【解析】
(1)根據(jù)題意和題目中的式子,可知x和y表示的實際意義;
(2)根據(jù)題意,選擇甲同學(xué)的方法進(jìn)行解答,注意分式方程要檢驗,也可選擇乙同學(xué)的作法,注意乙中求得y的值后,還要繼續(xù)計算,知道計算出原計劃平均每月的綠化面積結(jié)束.
解:(1)由題意可得, 甲同學(xué)所列方程中的x表示原計劃平均每月的綠化面積,乙同學(xué)所列方程中的y表示實際完成這項工程需要的月數(shù),
故答案為:原計劃平均每月的綠化面積;實際完成這項工程需要的月數(shù);
(2)甲:設(shè)原計劃平均每月綠化![]()
![]()
方程兩邊同乘以1.5x,得 90-60=3x,
解得,x=10,
經(jīng)檢驗,x=10是原分式方程的解,
答:原計劃平均每月的綠化面積是10km2.


 優(yōu)等生題庫系列答案
優(yōu)等生題庫系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】數(shù)學(xué)活動課上,小明同學(xué)根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗,對函數(shù)的圖像、性質(zhì)進(jìn)行了探究,下面是小明同學(xué)探究過程,請補充完整:
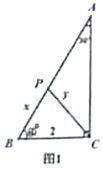
如圖1,已知在![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 為
為![]() 邊上的一個動點,連接
邊上的一個動點,連接![]() .設(shè)
.設(shè)![]() ,
,![]() .
.
(初步感知)
(1)當(dāng)![]() 時,則①
時,則①![]() ________,②
________,②![]() ________;
________;
(深入思考)
(2)試求![]() 與
與![]() 之間的函數(shù)關(guān)系式并寫出自變量
之間的函數(shù)關(guān)系式并寫出自變量![]() 的取值范圍;
的取值范圍;
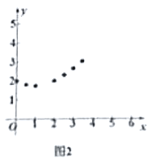
(3)通過取點測量,得到了![]() 與
與![]() 的幾組值,如下表:
的幾組值,如下表:
| 0 | 0.5 | 1 | 1.5 | 2. | 2.5 | 3 | 3.5 | 4 |
| 2 | 1.8 | 1.7 | _____ | 2 | 2.3 | 2.6 | 3.0 | _____ |
(說明:補全表格時相關(guān)數(shù)值保留一位小數(shù))
1)建立平面直角坐標(biāo)系,如圖2,描出已補全后的表中各對應(yīng)值為坐標(biāo)的點,畫出該函數(shù)的圖象;
2)結(jié)合畫出的函數(shù)圖象,寫出該函數(shù)的兩條性質(zhì):
①________________________________;②________________________________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,點A、B、C的坐標(biāo)分別為(-1,3)、(-4,1)、(-2,1),將△ABC沿一確定方向平移得到△A1B1C1,點B的對應(yīng)點B1的坐標(biāo)是(1,2),則點A1,C1的坐標(biāo)分別是( )
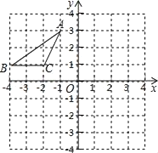
A.A1(4,4),C1(3,2)B.A1(3,3),C1(2,1)
C.A1(4,3),C1(2,3)D.A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
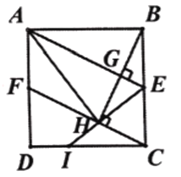
【題目】如圖1,正方形![]() 中, 點
中, 點![]() 是
是![]() 的中點,過點
的中點,過點![]() 作
作![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 垂直
垂直![]() 的延長線于點
的延長線于點![]() ,交
,交![]() 于點
于點![]() .
.
(1)求證:![]() ;
;
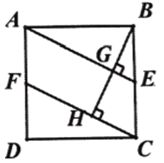
(2)如圖2,連接![]() ,連接
,連接![]() 并延長交
并延長交![]() 于點I,
于點I,
①求證:![]() ;
;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
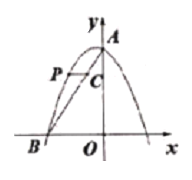
【題目】如圖,二次函數(shù)y=-x2+(n-1)x+3的圖像與y軸交于點A,與x軸的負(fù)半軸交于點B(-2,0)
(1)求二次函數(shù)的解析式;
(2)點P是這個二次函數(shù)圖像在第二象限內(nèi)的一線,過點P作y軸的垂線與線段AB交于點C,求線段PC長度的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】定義:在平面直角坐標(biāo)系中,![]() 為坐標(biāo)原點,
為坐標(biāo)原點,![]() 的邊
的邊![]() 平行于
平行于![]() 軸.若
軸.若![]() 的三個頂點都在二次函數(shù)
的三個頂點都在二次函數(shù)![]() 的圖像上,則稱
的圖像上,則稱![]() 為該二次函數(shù)圖像的“伴隨三角形”.
為該二次函數(shù)圖像的“伴隨三角形”.![]() 為拋物
為拋物![]() 的“伴隨三角形”.
的“伴隨三角形”.
(1)若點![]() 是拋物線與
是拋物線與![]() 軸的交點,求點
軸的交點,求點![]() 的坐標(biāo).
的坐標(biāo).
(2)若點![]() 在該拋物線的對稱軸上,且到邊
在該拋物線的對稱軸上,且到邊![]() 的距離為2,求
的距離為2,求![]() 的面積.
的面積.
(3)設(shè)![]() 兩點的坐標(biāo)分別為
兩點的坐標(biāo)分別為![]() ,比較
,比較![]() 與
與![]() 的大小,并求
的大小,并求![]() 的取值范圍.
的取值范圍.
(4)![]() 是拋物線
是拋物線![]() 的“伴隨三角形”,點
的“伴隨三角形”,點![]() 在點
在點![]() 的左側(cè),且
的左側(cè),且![]() ,點
,點![]() 的橫坐標(biāo)是點
的橫坐標(biāo)是點![]() 的橫坐標(biāo)的2倍,設(shè)該拋物線在
的橫坐標(biāo)的2倍,設(shè)該拋物線在![]() 上最高點的縱坐標(biāo)為
上最高點的縱坐標(biāo)為![]() ,當(dāng)
,當(dāng)![]() 時,直接寫出
時,直接寫出![]() 的取值范圍和
的取值范圍和![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 點
點![]() 在
在![]() 上,且
上,且![]() .動點
.動點![]() 同時從點
同時從點![]() 出發(fā),均以
出發(fā),均以![]() 的速度運動,其中點P沿
的速度運動,其中點P沿![]() 向終點
向終點![]() 運動;點
運動;點![]() 沿
沿![]() 向終點
向終點![]() 運動.過點
運動.過點![]() 作
作![]() 分交
分交![]() 于點
于點![]() ,設(shè)動點
,設(shè)動點![]() 運動的時間為
運動的時間為![]() 秒.
秒.
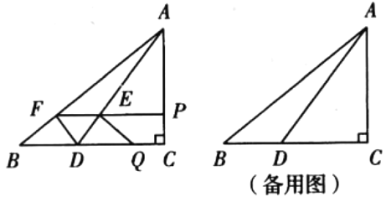
(1)求![]() 的長(用含
的長(用含![]() 的代數(shù)式表示);
的代數(shù)式表示);
(2)以點![]() 為頂點圈成的圍形面積為
為頂點圈成的圍形面積為![]() 求
求![]() 與
與![]() 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
(3)連接![]() 若點
若點![]() 為
為![]() 中點在整個運動過程中,直接寫出點
中點在整個運動過程中,直接寫出點![]() 運動的路徑長.
運動的路徑長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
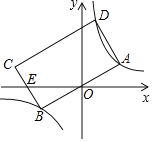
【題目】如圖,矩形ABCD的頂點A,B,D分別落在雙曲線y=![]() (k>0)的兩個分支上,AB邊經(jīng)過原點O,CB邊與x軸交于點E,且EC=EB,若點A的橫坐標(biāo)為1,則矩形ABCD的面積_____.
(k>0)的兩個分支上,AB邊經(jīng)過原點O,CB邊與x軸交于點E,且EC=EB,若點A的橫坐標(biāo)為1,則矩形ABCD的面積_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
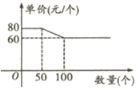
【題目】某批發(fā)部某一玩具價格如圖所示,現(xiàn)有甲、乙兩個商店,計劃在“六一”兒童節(jié)前到該批發(fā)部購買此類玩具,兩商店所需玩具總數(shù)為120個,乙商店所需數(shù)量不超過50個,設(shè)甲商店購買![]() 個,如果甲、乙兩商店分別購買玩具,兩商店需付款總和為
個,如果甲、乙兩商店分別購買玩具,兩商店需付款總和為![]() 元.
元.
(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式,并寫出自變量
的函數(shù)關(guān)系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(2)若甲商店購買不超過100個,請說明甲、乙兩商店聯(lián)合購買比分別購買最多可節(jié)約多少錢?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com