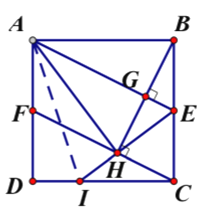
【題目】如圖1，正方形
中， 點
是
的中點，過點
作
于點
，過點
作
垂直
的延長線于點
，交
于點
．
（1）求證：
；
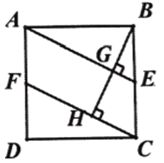
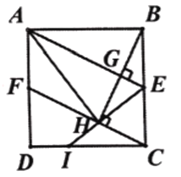
（2）如圖2，連接
，連接
并延長交
于點I，
①求證：
；
②求
的值．
【答案】（1）證明見解析；（2）①證明見解析；②
【解析】
（1）根據正方形的性質與已知條件證明
，利用AAS證明
；
（2）①結合（1）證明
，根據相似三角形的性質進行求證；
②方法一：延長
和
交于點
，由正方形的性質與已知條件得出四邊形
是平行四邊形，
，
，由①得出
，進而可求出
，最后根據相似三角形的性質進行求解；
方法二：連接
，利用直角三角形斜邊上的中線為斜邊的一半得出
，進而證明
，
，根據全等三角形的性質得出
，設
，
， 在
中利用勾股定理求出x，進而求解．
解：（1）證明：
四邊形
是正方形，
，
，
，
，
的延長線于點
，交于點
，
，
，
，
（AAS）；
（2）①證明：
，
又
，
即
，
，
，
，
；
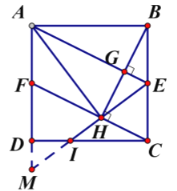
②方法一：如圖，延長和交于點，
，的延長線于點，交于點，
，
四邊形是正方形，
，
四邊形是平行四邊形，，，
，
點
是
中點，
在
中，
，
，
，
點是中點，
，
，
，
，
，
，
，
，
；
方法二：如圖， 連接，
點是中點，
，
，
，
，
，
，
，
又
，
，
，
，
，
，
，
設，，則
，
，
在中，由勾股定理得，
解得，
，
，
．
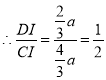科目：初中數學 來源： 題型：
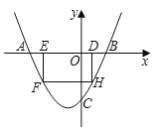
【題目】如圖，拋物線
與 x 軸交于點 A、B，與 y 軸交于點 C，且 OC＝2OB， 點 D 為線段 OB 上一動點(不與點 B 重合)，過點 D 作矩形 DEFH，點 H、F 在拋物線上，點 E 在 x 軸 上．
（1）求拋物線的解析式；
（2）當矩形 DEFH 的周長最大時，求矩形 DEFH 的面積；
（3）在（2）的條件下，矩形 DEFH 不動，將拋物線沿著 x 軸向左平移 m 個單位，拋物線與矩形 DEFH的邊交于點 M、N，連接 M、N．若 MN 恰好平分矩形 DEFH 的面積，求 m 的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
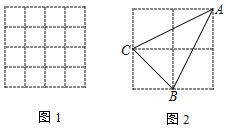
【題目】如圖1，每個小正方形的邊長都為1，點A、B、C在正方形網格的格點上，AB＝5，AC＝2，BC＝
．
（1）請在網格中畫出△ABC
（2）如圖2，直接寫出：
①AC＝ ，BC＝ ．
②△ABC的面積為 ．
③AB邊上的高為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】拋物線y=x2+2ax-3與x軸交于A、B(1，0)兩點(點A在點B的左側)，與y軸交于點C，將拋物線沿y軸平移m(m＞0)個單位，當平移后的拋物線與線段OA有且只有一個交點時，則m的取值范圍是_______________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下表是小安填寫的數學實踐活動報告的部分內容
題 目 | 測量鐵塔頂端到地面的高度 | |
測量目標示意圖 |
|
|
相關數據 | CD=20m，ɑ=45°，β=52° | |
求鐵塔的高度FE(結果精確到1米)（參考數據：sin52°≈0.79， cos52°≈0.62，tan52°≈1.28）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】題目：為了美化環境，某地政府計劃對轄區內
的土地進行綠化．為了盡快完成任務，實際平均每月的綠化面積是原計劃的1．5倍，結果提前2個月完成任務．求原計劃平均每月的綠化面積．
甲同學所列的方程為
乙同學所列的方程為
（1）甲同學所列的方程中
表示 ．乙同學所列的方程中
表示 ．
（2）任選甲、乙兩同學的其中一個方法解答這個題目．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，如圖，拋物線
與
軸交于
、
兩點，與直線
交于、
兩點，直線與
軸交于點
．
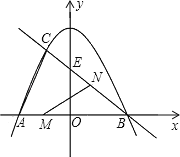
（1）求直線
的解析式：
（2）若點
在線段
上以每秒1個單位長度的速度從點向點運動（不與點、重合），同時，點
在射線上以每秒2個單位長度的速度從點向點方向運動，設運動的時間為
秒，
的面積為
，求關于的函數關系式，并求取何值時，最大？最大值是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司推出一款產品，經市場調查發現，該產品的日銷售量y（個）與銷售單價x（元）之間滿足一次函數關系，關于銷售單價，日銷售量，日銷售利潤的幾組對應值如表：
銷售單價x（元） | 85 | 95 | 105 | 115 |
日銷售量y（個） | 175 | 125 | 75 | 25 |
日銷售利潤w（元） | 875 | 1875 | 1875 | 875 |
（注：日銷售利潤＝日銷售量×（銷售單價﹣成本單價））
（1）求y與x的函數關系式；
（2）當銷售單價x為多少元時，日銷售利潤w最大？最大利潤是多少元？
（3）當銷售單價x為多少元時，日銷售利潤w在1500元以上？（請直接寫出x的范圍）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
