已知三角形三邊之比為2:3:4,且此三角形的三條中位線圍成的三角形的周長是9,則原三角形的最長邊是 .
【答案】
分析:此三角形的三條中位線等于原三角形三邊的一半,表示出三條中位線,讓其相加得9,即可求得最長的中位線,也就求出了最長的邊長.
解答:解:設三角形三邊分別為2x,3x,4x
∴三角形的三條中位線圍成的三角形的周長是

+
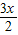
+
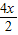
=9
解得:x=2
∴原三角形的最長邊是4×2=8.
故答案為8.
點評:此題屬中學階段常見題目,解答此題的關鍵是熟知三角形的三條中位線圍成的三角形的周長是原三角形的一半.
